5. Systèmes dynamiques : utilisation de SciPy¶
Contenu du chapitre
- Présentation du module SciPy
- Réalisation de traitements de données avancés avec SciPy
- Génération de figures avancées avec Matplotlib
- Ecrire la documentation d’une fonction
Dans les modules scientifiques de Python, il existe une collection impressionnante de fonctions réalisant des opérations diverses sur les tableaux numériques de NumPy. Il faut surtout les utiliser, plutôt que de réinventer la roue en recodant (probablement moins bien) une fonctionnalité qui existe déjà par ailleurs !
Dans NumPy, on a déjà vu qu’il existe beaucoup d’opérations permettant par exemple de
- générer des tableaux particuliers : np.arange, np.ones, np.linspace, ...
- faire des opérations à partir des valeurs du tableau : np.sum, np.sin, np.histogram, etc.
- exprimer des conditions (booléennes) sur les éléments d’un tableau ou extraire des parties d’un tableau : np.logical_not, np.in1d
- changer l’agencement des valeurs d’un tableau, sa forme, ou encore créer un nouveau tableau à partir de plusieurs autres : np.reshape, np.concatenate.
- etc. ...
Le module SciPy est la boîte à outils numérique pour les tableaux NumPy. On trouve dans SciPy les opérations de manipulation / traitement de données numériques classiques, mais spécifiques à un type d’application (algébre linéaire, statistiques, etc.). Ce sont donc des fonctions plus “haut niveau” que celles de NumPy.
SciPy est un module stable, bien testé et relativement bien documenté.
http://docs.scipy.org/doc/ http://docs.scipy.org/doc/scipy/reference/
>>> import scipy
Le module SciPy réalise les différentes opérations sur des tableaux numériques (ndarray) de numpy. On peut donc directement utiliser ces tableaux comme arguments pour les différentes fonctions
>>> from scipy import linalg
>>> mat = np.array([[1, 2], [2, 4]])
>>> mat
array([[1, 2],
[2, 4]])
>>> linalg.det(mat)
0.0
Pour montrer l’utilisation de SciPy, nous allons nous intéresser à l’intégration d’équations différentielles, en considérant des systèmes dynamiques à base de pendules mécaniques.
5.1. Pendule simple¶
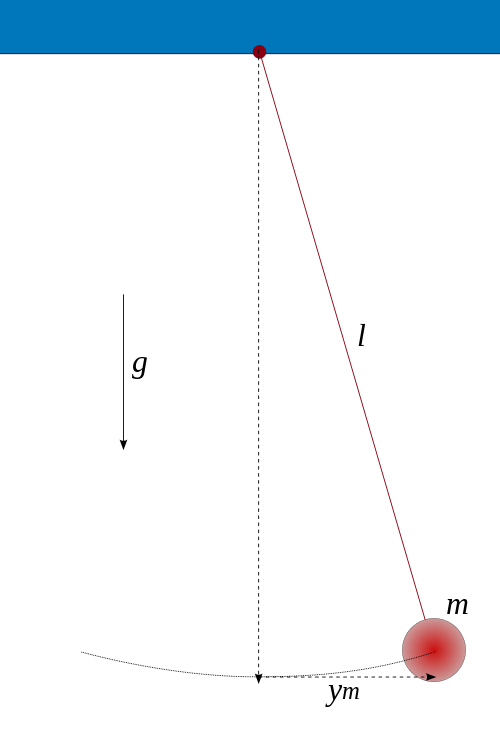
En écrivant la relation fondamentale de la dynamique (conservation de la quantité de mouvement), on obtient l’équation du pendule simple donnée par
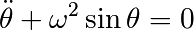
où 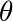 est l’angle du pendule par rapport à la verticale, et
on note avec un point la dérivée temporelle.
est l’angle du pendule par rapport à la verticale, et
on note avec un point la dérivée temporelle.
Pour les petites oscillations on peut faire l’approximation
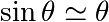 . Quand l’approximation n’est pas valide il
faut intégrer numériquement cette équation différentielle pour obtenir
l’évolution de la position et de la vitesse angulaire du pendule, au
cours du temps.
. Quand l’approximation n’est pas valide il
faut intégrer numériquement cette équation différentielle pour obtenir
l’évolution de la position et de la vitesse angulaire du pendule, au
cours du temps.
Il nous faut donc disposer d’un intégrateur d’équations différentielles, que l’on peut s’attendre à trouver dans SciPy. Mais quelle est la fonction correspondante ? Tentons une recherche Google “scipy integrate differential equation”, ou la consultation du sommaire de l’aide http://docs.scipy.org/doc/scipy/reference/index.html. Il existe un sous-module integrate, qui contient lui-même une fonction odeint
from scipy.integrate import odeint
Regarder la doc de la fonction http://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.odeint.html#scipy.integrate.odeint et l’exemple http://docs.scipy.org/doc/scipy/reference/tutorial/integrate.html#ordinary-differential-equations-odeint
Pour commencer, il faut mettre l’équation différentielle du 2nd ordre sous la forme d’un système d’équations du premier ordre
def simple_pendulum(theta_thetadot, t):
theta, theta_dot = theta_thetadot
return [theta_dot, - np.sin(theta)]
correspondant à
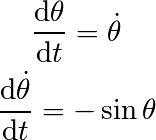
Nous pouvons maintenant intégrer une trajectoire à partir d’une condition initiale
>>> t = np.linspace(0, 5 * np.pi, 1000)
>>> sol = odeint(simple_pendulum, (np.pi/3, 0), t)
Attention
Comme la fonction odeint, il existe un grand nombre de fonctions permettant de réaliser des opérations haut niveau de calcul scientifique.
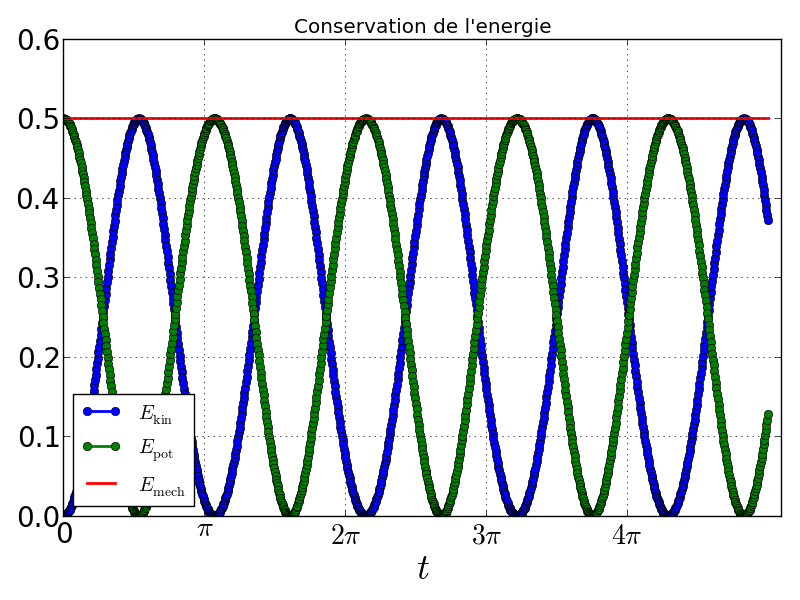
Nous pouvons par exemple vérifier la conservation de l’énergie mécanique au cours du temps
>>> theta, theta_dot = sol.T
>>> E_kin = 1./ 2 * theta_dot ** 2
>>> E_pot = 1 - np.cos(theta) # z
>>> E_mech = E_kin + E_pot
>>> plt.plot(t, E_kin, 'o-', lw=2, label=u'$E_\mathrm{kin}$')
>>> plt.plot(t, E_pot, 'o-', lw=2, label=u'$E_\mathrm{pot}$')
>>> plt.plot(t, E_mech, lw=2, label=u'$E_\mathrm{mech}$')
>>> plt.legend()
Pour générer la figure ci-dessus, on a utilisé un certain nombre de commandes du module matplotlib.
Pour construire les différents éléments de la figure (courbe, labels, légende, etc.), il existe des fonctions dédiées de matplotlib qu’on peut “découvrir” grâce à la documentation de matplotlib http://matplotlib.org/. En particulier, la gallerie d’exemples http://matplotlib.org/gallery.html est très utile pour voir comment générer différents types de figures.
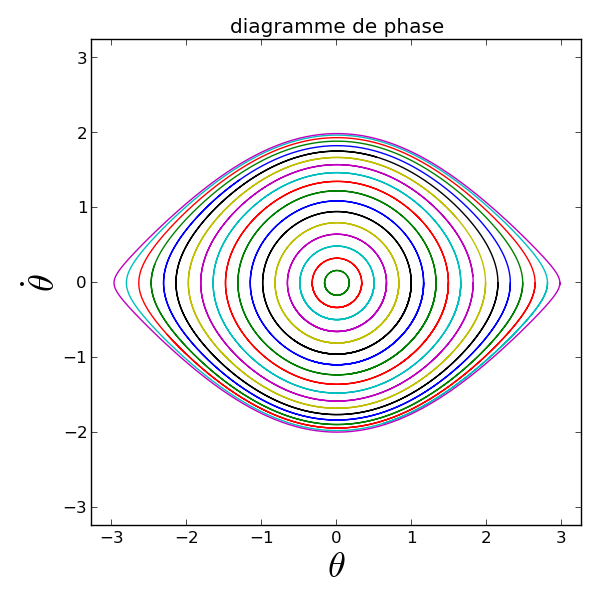
Exercice
Ecrire un script python pour construire le diagramme des phases du pendule simple, représenté ci-dessous. Pour celà, il faut
- intégrer l’équation différentielle pour différentes conditions initiales entre 0 et
.
- représenter
en fonction de
pour les différentes solutions.
5.2. Pendule forcé¶
On peut rajouter un degré de liberté au système dynamique du pendule en imposant un forçage dépendant du temps, par exemple périodique en temps. Nous allons également considérer un amortissement du pendule dû au frottement de l’air. On considère alors l’équation suivante pour le pendule forcé
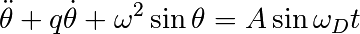
Comme auparavant, on normalise le temps en fixant 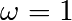 . Il
reste alors trois paramètres sur lesquels on peut jouer : A, q et
. Il
reste alors trois paramètres sur lesquels on peut jouer : A, q et
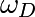 . On définit donc une nouvelle fonction définissant le
système dynamique du premier ordre
. On définit donc une nouvelle fonction définissant le
système dynamique du premier ordre
def forced_pendulum_equations(y, t, q, acc, omega):
theta, theta_dot = y
return [theta_dot, acc * np.sin(omega * t) - \
np.sin(theta) - q * theta_dot]
Par commodité, on va également définir une fonction permettant d’intégrer une trajectoire à partir d’une condition initiale, sur un certain intervalle de temps:
def forced_pendulum(t_end, t_space, theta_init, theta_dot_init=0, q=0.1,
acc=1, omega=1):
t_range = np.arange(0, t_end, t_space)
sol = odeint(forced_pendulum_equations, [theta_init, theta_dot_init],
t_range, args=(q, acc, omega))
return np.vstack((t_range, sol.T))
On peut à présent intégrer une trajectoire:
omega = 2./3
dt = 2*np.pi / omega / 25
tf = 1000
t, theta_0, theta_dot_0 = forced_pendulum(tf, dt, np.pi/3, 0,
q=0.5, acc=1, omega=omega)
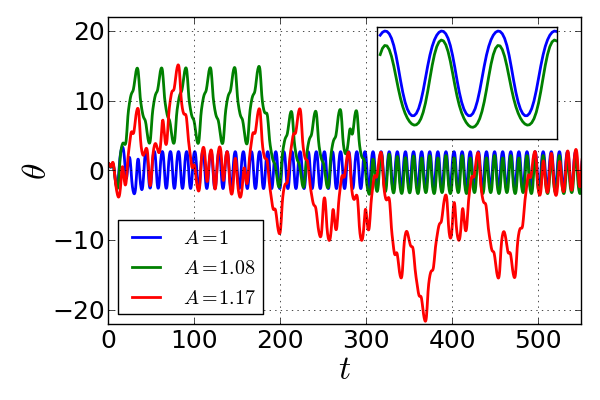
Pour cette trajectoire, l’évolution de 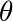 reste périodique,
avec la même période que la période de forçage
reste périodique,
avec la même période que la période de forçage
import matplotlib.pyplot as plt
plt.plot(t, theta_0) # courbe bleue
Quand on augmente l’amplitude du forçage, le mouvement reste périodique après un régime transitoire assez long. On observe par contre un doublement de période, l’amplitude de l’oscillation varie entre deux périodes du forçage
t, theta_1, theta_dot_1 = forced_pendulum(tf, dt, np.pi/3, 0,
q=0.5, acc=1.08, omega=omega)
plt.plot(t, theta_1) # courbe verte
Enfin, quand on augmente encore l’amplitude du forçage, le mouvement n’est plus périodique et semble “chaotique”:
t, theta_2, theta_dot_2 = forced_pendulum(tf, dt, np.pi/3, 0,
q=0.5, acc=1.17, omega=omega)
plt.plot(t, theta_2) # courbe rouge
On va confirmer l’observation du doublement de période grâce à la transformée de Fourier discrète des signaux. Pour la transformée de Fourier discrète, il existe également un sous-module de SciPy:
>>> from scipy import fftpack
Il faut tout d’abord sélectionner la partie du signal qui semble périodique, c’est-à-dire enlever le régime transitoire. On utilise pour cela un masque de booléens
>>> time_mask = t > 400
>>> theta_0 = theta_0[time_mask]
Comme on n’est pas intéressé par la fréquence nulle, on soustrait la moyenne du signal
>>> theta_0 -= theta_0.mean()
Notons qu’on peut soustraire un scalaire à un tableau ndarray : la soustraction est alors faite élément par élément.
On calcule la transformée de Fourier discrète de 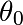 :
:
>>> fft_theta_0 = fftpack.fft(theta_0)
Pour représenter la TF, il nous faut également un tableau des fréquences correspondant au tableau fft_theta_0. Il y a pour cela une fonction dédiée dans le module fftpack, fftfreq:
>>> freq = fftpack.fftfreq(len(theta_0), dt)
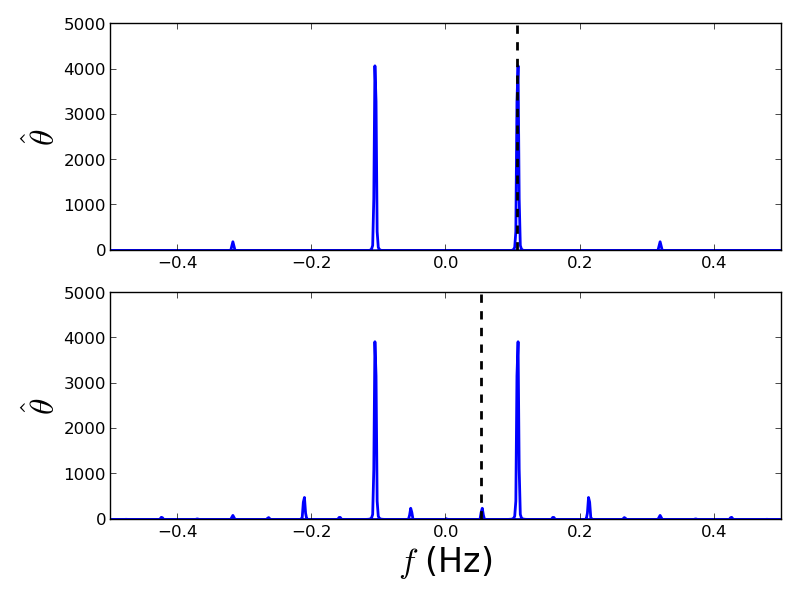
On peut alors représenter le module de la transformée de Fourier en fonction de la fréquence
>>> plt.plot(freq, np.abs(fft_theta_0), lw=2)
On observe que la fréquence fondamentale du signal correspond à la
fréquence de forçage 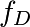 . On observe aussi une harmonique triple
à
. On observe aussi une harmonique triple
à 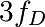 .
.
Pour le forçage intermédiaire, on refait la même série d’opérations
theta_1 = theta_1[time_mask]
theta_1 -= theta_1.mean()
fft_theta_1 = fftpack.fft(theta_1)
plt.plot(freq, np.abs(fft_theta_1), lw=2)
On observe alors un nouveau pic à la fréquence moitiés 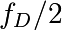 ,
correspondant à un doublement de période.
,
correspondant à un doublement de période.
Pour aller plus loin, on peut visualiser l’évolution du spectre de
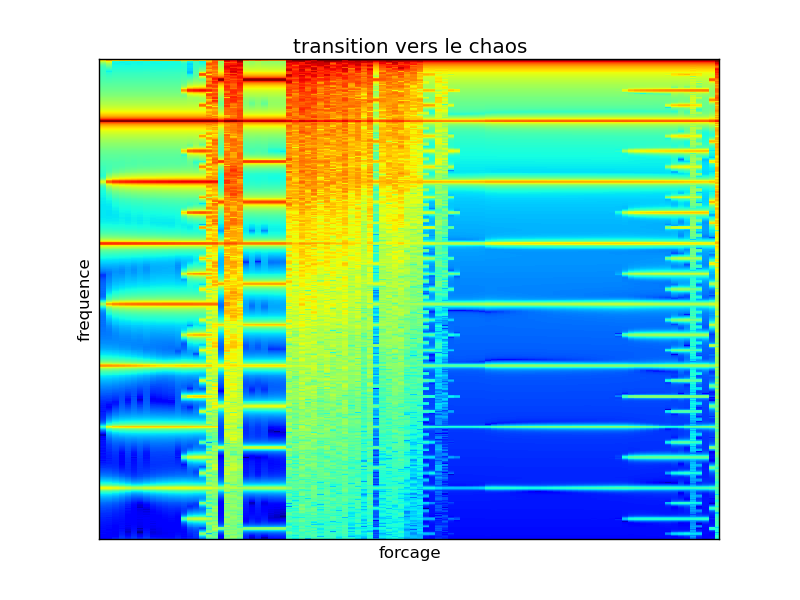
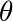 pour un grand nombre de paramètres en codant par la couleur l’amplitude du module de la transformée de Fourier:
pour un grand nombre de paramètres en codant par la couleur l’amplitude du module de la transformée de Fourier:
>>> omega = 2./3
>>> dt = 2*np.pi / omega / 25
>>> tf = 1000
>>> acc_factors = np.linspace(1, 1.5, 100)
>>> fft_sig = []
>>>
>>> t = np.arange(0, tf, dt)
>>> mask = t > 400
>>> hann = signal.hanning(mask.sum())
>>>
>>> for i, acc in enumerate(acc_factors):
>>> print i
>>> t, theta, theta_dot = forced_pendulum(tf, dt, np.pi/3, 0,
>>> q=0.5, acc=acc, omega=omega)
>>> theta = theta[mask]
>>> theta -= theta.mean()
>>> theta /= np.sqrt((theta**2).mean())
>>> theta *= hann
>>> fft_sig.append(fftpack.fft(theta))
>>>
>>> fft_sig = np.array(fft_sig)
>>> plt.imshow(np.log(np.abs(fft_sig[:, :500]).T), aspect='auto',
interpolation='nearest')
On observe alors la cascade de transition vers le chaos, avec des fenêtre chaotiques et d’autres périodiques.
Exercice
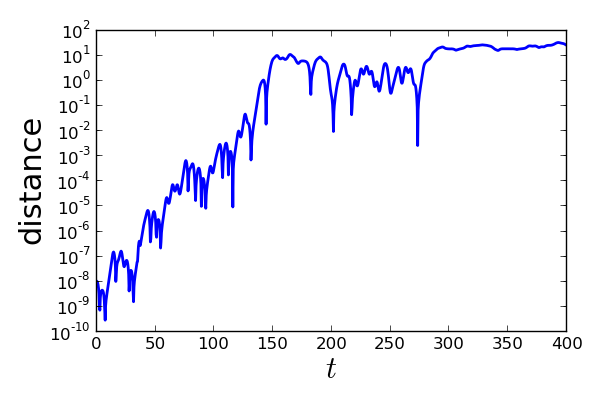
Une propriété des systèmes dynamiques chaotiques est leur grande sensibilité aux conditions initiales : deux trajectoires initialement très proches vont d’éloigner exponentiellement vite au cours du temps.
Dans le régime chaotique, on va vérifier que deux trajectoires initialement très proches s’éloignent très vite. Pour les paramètres
omega = 2./3
acc = 1.17
q = 0.5
eps = 1.e-8
initialiser deux trajectoires séparées par une distance eps
(conditions initiales 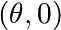 et
et
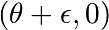 , par exemple), et représenter leur
distance dans l’espace des phases au cours du temps
, par exemple), et représenter leur
distance dans l’espace des phases au cours du temps
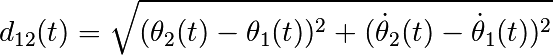
Pour vérifier que la distance grandit de manière exponentielle au cours du temps, faire une représentation graphique en coordonnées semi-logarithmiques (plt.semilogy).
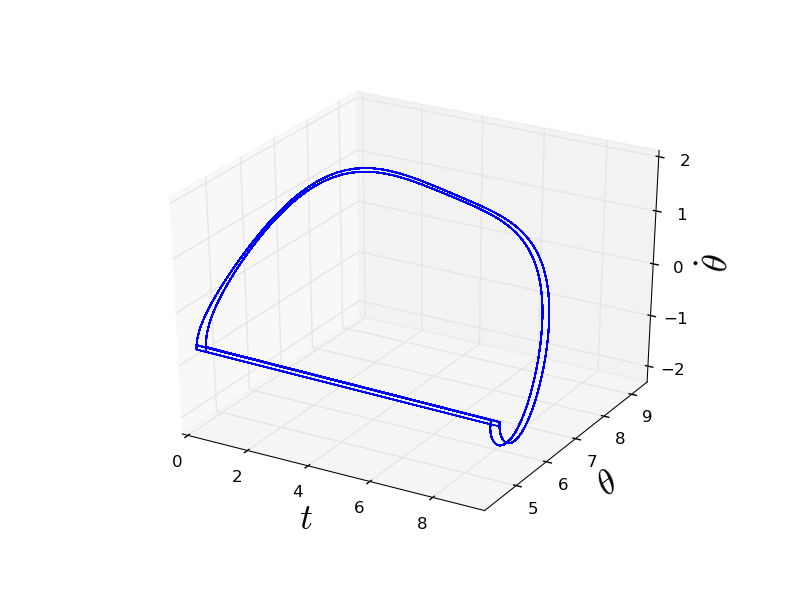
Pour aller plus loin
On peut représenter en 3-D le cycle limite décrivant la dynamique du pendule.
5.3. Input/output : comment sauver des tableaux, et charger des fichiers¶
Pour le moment, nous n’avons pas encore sauvé aucun de nos résultats ! On peut facilement sauver un tableau NumPy sous deux formats :
- en texte ascii avec np.savetxt (si on a besoin de voir le tableau dans un éditeur de texte) pour les tableaux de dimension <= 2.
- en format binaire de NumPy avec np.save (pour des fichiers moins gros en mémoire)
>>> a = np.arange(25).reshape((5, 5))
>>> a
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19],
[20, 21, 22, 23, 24]])
>>> np.savetxt('tableau.txt', a)
>>> np.save('tableau.npy', a)
>>> import os
>>> os.path.getsize('tableau.txt')
625
>>> os.path.getsize('tableau.npy')
280
Pour des tableaux de dimension trois ou plus, il faut utiliser np.save
>>> b = np.ones((2, 1, 3, 4))
>>> b.shape
(2, 1, 3, 4)
>>> np.savetxt('b.txt', b)
Traceback (most recent call last):
File "<ipython-input-13-1d7a297e3d85>", line 1, in <module>
np.savetxt('b.txt', b)
File "/usr/lib/python2.7/dist-packages/numpy/lib/npyio.py", line 979,
in savetxt
fh.write(asbytes(format % tuple(row) + newline))
TypeError: float argument required, not numpy.ndarray
>>> np.save('b.npy', b)
De la même manière, il existe deux fonctions pour charger un tableau numpy à partir d’un fichier
>>> c = np.loadtxt('tableau.txt')
>>> d = np.load('tableau.npy')
Remarque
La librairie standard de Python permet de sauver n’importe quelle string dans un fichier .
Des modules spécialisés peuvent permettrent de sauver des tableaux dans d’autres format : csv, hdf5, etc.
5.4. Ecriture de documentation¶
Dans l’exemple précédent du pendule forcé, la fonction forced_pendulum est une fonction haut niveau, que l’utilisateur final va souvent manipuler. Pour cela, il est recommandé d’écrire une bonne documentation pour la fonction forced_pendulum. Il existe un standard pour l’écriture de docstrings hérité de NumPy, et documenté sur https://github.com/numpy/numpy/blob/master/doc/HOWTO_DOCUMENT.rst.txt. Les différentes sections sont toujours dans le même ordre, ce qui permet une lecture rapide et efficace de la documentation:
def forced_pendulum(t_end, t_space, theta_init, theta_dot_init=0, q=0.1,
acc=1, omega=1):
"""
Integrate a trajectory for the forced pendulum.
Parameters
----------
t_end : float
Final time of the trajectory (initial time is always 0).
t_space : float
Time_interval between two points of the trajectories
theta_init : float
Initial angular position
theta_dot_init : float, optional
Initial angular velocity (default 0)
q : float, optional
Damping (default 0.1)
acc : float, optional
Amplitude of the forcing (default 1)
omega : float, optional
Pulsation of forcing (default 1)
Returns
-------
t: ndarray of floats
array of times
theta: ndarray of floats
angular positions along the trajectory
theta_dot: ndarray of floats
angular velocities along the trajectory
Notes
-----
This function integrates the equation
.. math::
\ddot{\\theta} + q \dot{\\theta} + \omega^2 \sin\\theta = A \sin
\omega_D t
Examples
--------
>>> t, theta, theta_dot = forced_pendulum(100, 0.1, np.pi/3)
>>> sol = forced_pendulum(100, 0.1, np.pi/3, theta_dot_init=1, acc=1.5)
"""
t_range = np.arange(0, t_end, t_space)
sol = odeint(forced_pendulum_equations, [theta_init, theta_dot_init],
t_range, args=(q, acc, omega))
return np.vstack((t_range, sol.T))