7.1.2. Mini-tutoriel de traitement d’images

Le module skimage est organisé en plusieurs sous-modules correspondant à plusieurs branches du traitement d’images : segmentation, filtrage, gestion des formats d’image, etc. Pour éviter d’avoir des noms trop longs, on importe souvent directement les sous-modules dans le namespace principal

>>> from skimage import data
>>> coins_image = data.coins()
>>> from skimage import io
>>> io.imshow(coins_image)
>>> from skimage import filter
>>> edges = filter.sobel(coins_image)

La grande majorité des fonctions de skimage se trouvent donc à l’intérieur d’un sous-module : il y a deux niveaux hiérarchiques.

7.1.2.1. Input / output: des fichiers aux tableaux numpy

>>> import os
>>> import skimage
>>> current_dir = os.getcwd() # so that we can go back to current dir.
>>> os.chdir(skimage.data_dir)

On peut ouvrir un fichier image (jpg, png, tiff...) comme un tableau numpy en passant le chemin du fichier à la fonction skimage.io.imread

>>> from skimage import io
>>> coins_image = io.imread('coins.png')

Une large gamme de formats de fichier est supportée : jpg, png, tiff, bmp, etc.

On peut ouvrir des images en couleur ou en noir et blanc. Les images en couleur ont trois dimensions, les images en noir et blanc en ont deux

>>> coins_image.shape
(303, 384)
>>> lena_image = io.imread('lena.png')
>>> lena_image.shape
(512, 512, 3)
>>> io.imshow(lena_image) # color image
>>> io.imshow(lena_image[..., 0]) # grayscale image

L’affichage d’une image se fait grâce à la fonction skimage.io.imshow.

On peut aussi ouvrir une image couleur comme une image en noir et blanc

>>> lena_gray = io.imread('lena.png', as_grey=True)
>>> lena_gray.shape
(512, 512)
>>> os.chdir(current_dir)

Type des tableaux d’image

Les tableaux d’images peuvent être soit des tableaux d’entier, soit des tableaux de flottants. La plupart des formats d’image stockent les valeurs des pixels sous forme d’entiers; le format le plus classique correspond à des entiers codés sur 8 bits (entre 0, et 255), ce qui correspond au type np.uint8 de numpy (entier non signé sur 8 bits).

Il est par contre naturel d’utiliser des flottants dès qu’on fait des opérations sur les pixels dans l’espace des réels, comme des multiplications ou des divisions par des réels. Par conséquent, certaines fonctions de skimage renvoient un tableau de type différent du tableau d’entrée

>>> from skimage import data
>>> coins_image = data.coins()
>>> coins_image.dtype
dtype('uint8')
>>> median_filter_coins = median_filter(coins_image)
>>> median_filter_coins.dtype # median of integers is an integer
dtype('uint8')
>>> from skimage import exposure
>>> equalize_coins = exposure.equalize(coins_image)
>>> equalize_coins.dtype
dtype('float64')

Dans skimage, par convention les images en flottant sont à valeur entre -1 et 1, afin d’assurer que toutes les images aient la même plage de valeurs. La plage de valeurs d’une image retournée par une fonction peut donc être très différente de celle de l’image d’entrée, dans le cas où le type a été modifié

>>> print coins.min(), coins.max()
1 252
>>> print equalize_coins.min(), equalize_coins.max()
8.59460946095e-06 1.0

Les fonctions skimage.img_as_float et skimage.img_as_ubyte permettent de faire la conversion entre les types sans se soucier des changements d’échelle.

De la même manière qu’on peut ouvrir un fichier image comme tableau numpy, on peut faire l’opération contraire : sauver un tableau numpy correspondant à une image en un fichier image. Pour cela, on utilise la fonction skimage.io.imsave

>>> io.imsave('equalize_coins.png', equalize_coins)

Le type du fichier image est automatiquement déduit de l’extension de la chaîne de caractères (‘.png’, ‘.jpg’).

7.1.2.2. Quelques opérations de base avec numpy

Une fois que notre image est un tableau numpy, les opérations de numpy sur les éléments du tableau correspondent à des opérations sur les pixels.

>>> path = os.path.join(skimage.data_dir, 'lenagray.png')
>>> lena = io.imread(path)
>>> # Pixel value
>>> lena[20, 32]
110
>>> # Slicing
>>> lena[20:22, 32:34]
Image([[110, 113],
    [110, 111]], dtype=uint8)
>>> lena[50:60] = 255
>>>
>>> lx, ly = lena.shape
>>> X, Y = np.ogrid[0:lx, 0:ly]
>>> mask = (X - lx/2)**2 + (Y - ly/2)**2 > lx*ly/4
>>> # Using masks
>>> lena[mask] = 0

Attention : pour l’indexation, la 1e dimension (axe 0) correspond aux lignes indicées de haut en bas, et la 2e dimension (axe 1) correspond aux colonnes de gauche à droite. C’est la convention des tableaux numpy.

Exercice

Cet exercice a pour but de s’entraîner 1) au slicing des tableaux numpy et 2) à la représentation d’images couleurs sous la forme de tableaux numpy à trois canaux.

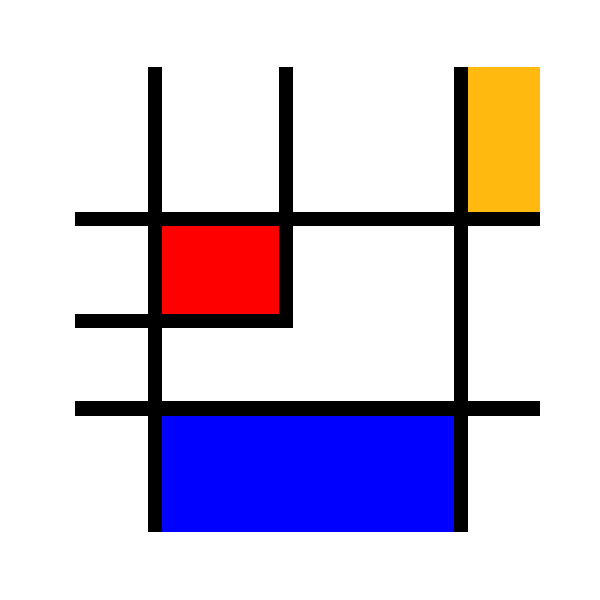
Exercice : réaliser une image ressemblant à l’image ci-dessus, sous la forme d’un tableau numpy. On pourra par exemple prendre l’image de forme 32x32, et de type np.uint8 (entiers de 0 à 255).

Indices :

• Les trois canaux de couleur sont dans l’ordre R, V, B (rouge vert bleu).
• Le jaune correspond au triplet (R, V, B) = (255, 185, 15)

Voir la solution :

[Python source code]

7.1.2.3. Filtrage d’image

Le filtrage consiste (au sens large) à transformer une image par une autre image, en remplaçant la valeur d’un pixel par une fonction de cette valeur mais aussi des valeurs des autres pixels de l’image. On dit que le filtre est local si ce sont les valeurs des pixels voisins qui sont utilisées, non-local sinon:

>>> from skimage import filter

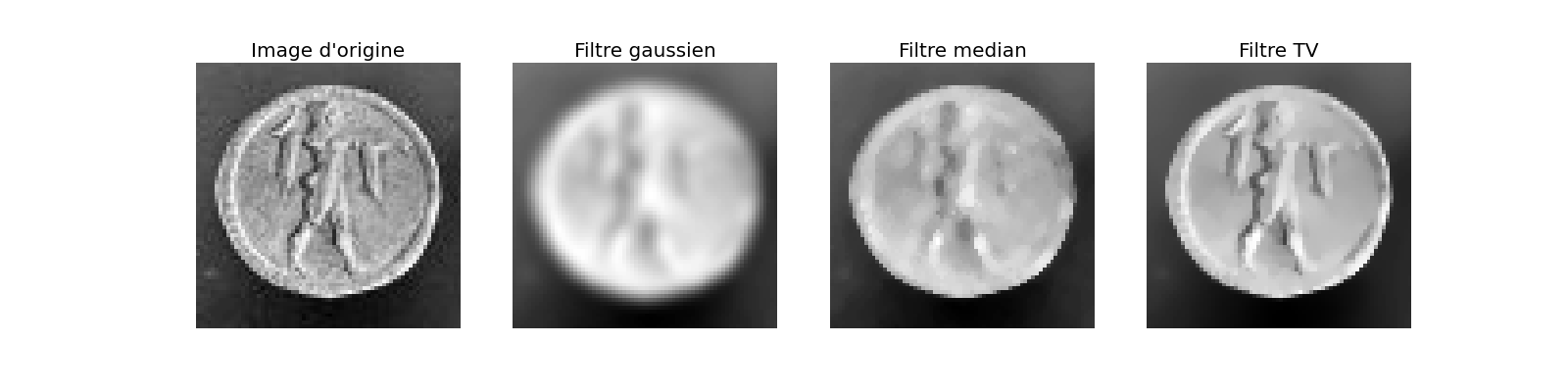
Il existe en particulier un certain nombre de fonctions qui vont moyenner ensemble des pixels proches. Cela peut être utile dans des applications de débruitage, où on veut réduire le bruit sur les pixels:

>>> coins_zoom = coins[10:80, 300:370]
>>> median_coins = filter.median_filter(coins_zoom)
>>> tv_coins = filter.tv_denoise(coins_zoom, weight=0.1)

Attention : le filtre gaussien ne se trouve pas dans scikit-image, mais dans scipy.ndimage

>>> from scipy import ndimage
>>> gaussian_coins = ndimage.gaussian_filter(coins, sigma=2)

Un autre type de filtrage très pratique est la morphologie mathématique : ce sont des opérations logiques locales sur des ensembles de pixels. Ces opérations peuvent fonctionner sur des images d’entiers (0 à 255), mais par simplicité nous allons uniquement voir des opérations qui fonctionnent sur des images binaires de 0 et de 1 (False et True) : c’est la morphologie mathématique binaire.

La plupart des opérations reposent sur un élément structurant, qui va servir à sonder l’image binaire.

>>> morphology.disk(1)
array([[0, 1, 0],
    [1, 1, 1],
    [0, 1, 0]], dtype=uint8)
>>> morphology.disk(3)
array([[0, 0, 0, 1, 0, 0, 0],
    [0, 1, 1, 1, 1, 1, 0],
    [0, 1, 1, 1, 1, 1, 0],
    [1, 1, 1, 1, 1, 1, 1],
    [0, 1, 1, 1, 1, 1, 0],
    [0, 1, 1, 1, 1, 1, 0],
    [0, 0, 0, 1, 0, 0, 0]], dtype=uint8)

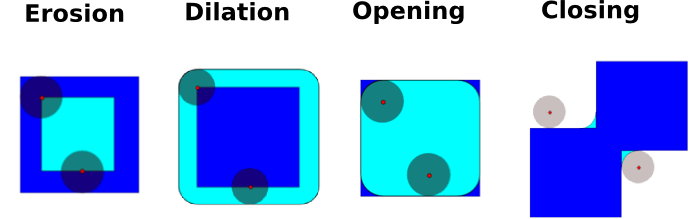
L’opération d’érosion va venir éroder les objets (de valeur 1) de l’image : quand on centre l’élément structurant sur un pixel donné, on met ce pixel à 0 si tous les pixels recouverts par l’élément structurant ne sont pas à 1.

>>> a = np.zeros((7, 7))
>>> a[1:-1, 1:-1] = 1
>>> a
array([[ 0.,  0.,  0.,  0.,  0.,  0.,  0.],
    [ 0.,  1.,  1.,  1.,  1.,  1.,  0.],
    [ 0.,  1.,  1.,  1.,  1.,  1.,  0.],
    [ 0.,  1.,  1.,  1.,  1.,  1.,  0.],
    [ 0.,  1.,  1.,  1.,  1.,  1.,  0.],
    [ 0.,  1.,  1.,  1.,  1.,  1.,  0.],
    [ 0.,  0.,  0.,  0.,  0.,  0.,  0.]])
>>> erosion_a = morphology.binary_erosion(a, morphology.disk(1))
>>> erosion_a
array([[False, False, False, False, False, False, False],
    [False, False, False, False, False, False, False],
    [False, False,  True,  True,  True, False, False],
    [False, False,  True,  True,  True, False, False],
    [False, False,  True,  True,  True, False, False],
    [False, False, False, False, False, False, False],
    [False, False, False, False, False, False, False]], dtype=bool)
>>> morphology.binary_erosion(a, morphology.disk(3))
array([[False, False, False, False, False, False, False],
    [False, False, False, False, False, False, False],
    [False, False, False, False, False, False, False],
    [False, False, False, False, False, False, False],
    [False, False, False, False, False, False, False],
    [False, False, False, False, False, False, False],
    [False, False, False, False, False, False, False]], dtype=bool)

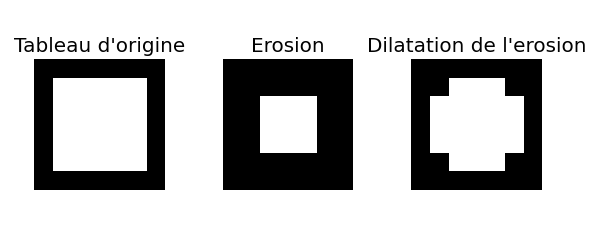
L’opération contraire s’appelle la dilatation : la dilatation met à 1 tous les pixels pour lesquels l’éléments structurant centré au pixel recouvre au moins un pixel valant 1

dilation_erosion_a = morphology.binary_dilation(erosion_a,
                         morphology.disk(1))

On voit que la composition d’une érosion puis d’une érosion redonne presque l’image d’origine, à l’exception des coins qui ont disparu. Cette opération s’appelle une ouverture. De même, une ouverture va faire disparaître les petits objets, qui disparaîtront à l’érosion et ne pourront donc pas être dilatés lors de l’étape de dilatation.

7.1.2.4. Extraction d’objets d’intérêt

Une tâche classique consiste à séparer une image en un nombre fini de régions, en attribuant à chaque pixel une étiquette (un “label”) correspondant au numéro de la région.

Par exemple, on peut vouloir binariser une image en régions claires et sombres. Il existe dans scikit-image une fonction calculant automatiquement le seuil le plus discriminant entre deux populations de pixels : la fonction skimage.filter.threshold_otsu qui implémente l’algorithme de seuillage d’Otsu

from skimage import data
from skimage import filter
camera = data.camera()
val = filter.threshold_otsu(camera)
mask = camera < val

Parfois, un simple seuillage sur toute l’image ne donne pas un résultat satisfaisant ; c’est notamment le cas lorsque l’éclairage de l’image n’était pas homogène. Il existe donc une fonction qui va calculer le seuil dans un voisinage local, et peut donc binariser une image de façon plus satisfaisante

simple_threshold = coins > filter.threshold_otsu(coins)
adaptive_threshold = filter.threshold_adaptive(coins, 151)

L’image adaptive_threshold a bien séparé les pièces du fond, pour supprimer les petites taches blanches et la bande en haut de l’image on peut utiliser deux fonctions du scikit-image dont le nom donne la fonction : remove_small_objects et clear_border:

from skimage import segmentation
from skimage import morphology
filter_res = morphology.remove_small_objects(adaptive_threshold)
clear_image = segmentation.clear_border(filter_res)

Il existe dans scikit-image des algorithmes de segmentation beaucoup plus sophistiqués que les seuillages, par exemple des algorithmes de croissance de région à partir de pixels marqueurs, ou des décompositions automatiques de l’image en “super-pixels”. La meilleure manière de se familiariser avec ces algorithmes consiste à consulter les exemples de la gallerie du scikit-image.

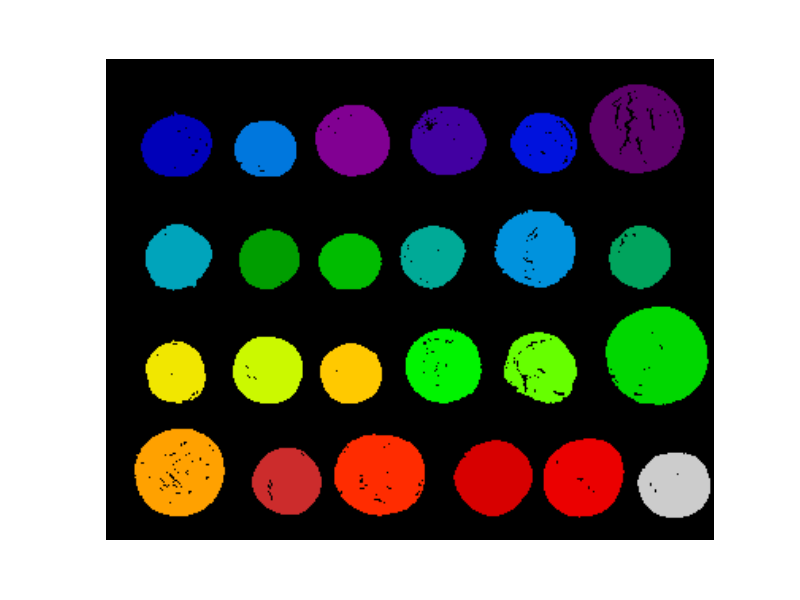
Une fois qu’on a binarisé l’image, on peut donner un indice différent à chaque objet séparé (composante connexe) grâce à la fonction morphology.label

labels = morphology.label(clear_image, background=0)

7.1.2.5. Mesure des propriétés des objets

Une fois qu’on a séparé une image en régions avec différents indices, on peut aller calculer différentes propriétés de ces régions grâce à la fonction skimage.measure.regionprops

from skimage import measure
props = measure.regionprops(labels, ['Area'])

>>> props[0]
{'Area': 1652.0, 'Label': 1}
>>> (labels == 1).sum()
1652

7.1.2.6. Et autres

On n’a fait ici qu’effleurer certains aspects du traitement d’images, il existe dans scikit-image bien d’autres possibilités pour aller reconnaître des formes dans une image, appliquer des déformations à des images, extraire des descripteurs d’images pour les classifier automatiquement, etc. On peut déjà en apprendre pas mal en allant lire (et faire !) les exemples du scikit-image.