7.1.3. Géométrie d’un matériaux granulaire 2-D

---

Les matériaux granulaires sont omni-présents dans l’industrie et l’environnement. La science des matériaux granulaires est relativement récente car elle a nécessité des techniques d’instrumentation et de simulation qui n’ont fait leur apparition que tard.

Dans cet atelier, on va s’intéresser à la géométrie d’un matériau granulaire en deux dimensions, c’est-à-dire :

• à la fraction de l’espace occupée par les grains, appelée la compacité du milieu granulaire
• au nombre de voisins de chaque grain

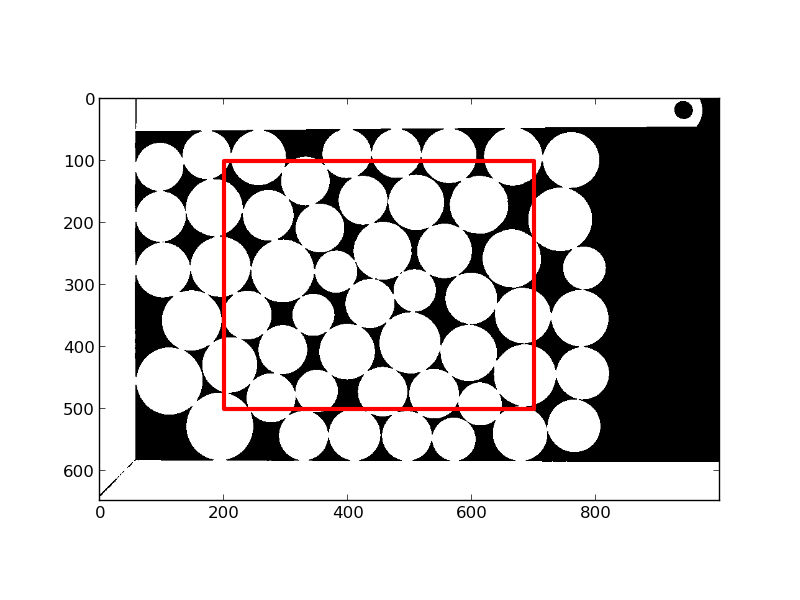
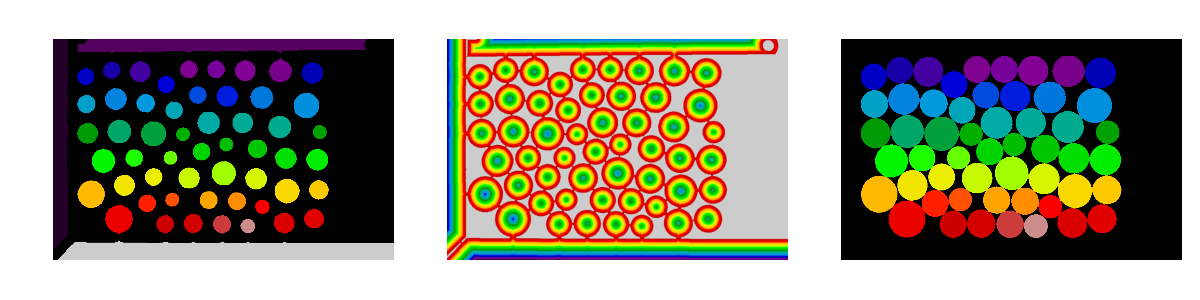
Le matériau granulaire 2-D est un ensemble de pièces de monnaie, ci-dessus on voit le matériau granulaire photographié avec deux éclairages différents. Pour l’atelier on se servira de l’image la plus contrastée. On pourra plus tard se convaincre de l’importance de l’éclairage en essayant de reproduire les opérations sur l’autre image !

[Solution de tout l’atelier]

7.1.3.1. Ouverture de l’image comme un tableau NumPy

Sauver l’image contrastée ci-dessus (clic droit, sauver sous) dans le répertoire de travail. Ouvrir l’image comme un tableau Numpy appelé img avec la fonction skimage.io.imread.

Afficher l’image avec skimage.io.imshow.

Quelle est la forme de l’image ? Le maximum des valeurs des pixels ? Le minimum ?

7.1.3.2. Binarisation de l’image

On veut à présent séparer l’image en deux parties, 1) le fond et 2) les objets.Comme nous partons d’une image très contrastée, un simple seuillage va suffire pour donner un bon résultat.

• Utiliser la fonction skimage.filter.threshold_otsu pour choisir la valeur à laquelle seuiller l’image. Optionnel : tracer l’histogramme de l’image pour vérifier que cette valeur est cohérente avec celle qu’on aurait choisi “à la main”.
• Créer une image booléenne mask qui vaut 1 pour les pixels inférieurs au seuil dans l’image originale, et 0 pour les autres. On a ainsi créé une binarisation de l’image en fond (à 0) et objets (à 1)
• On peut maintenant calculer la compacité du matériau granulaire en calculant la fraction de l’espace occupée par des pixels des objets. Pour s’affranchir des effets de bord, calculer cette fraction dans un rectangle intérieur loin des bords (comme le rectangle rouge ci-dessous)

7.1.3.3. Séparation des différents grains

On souhaite maintenant attribuer les différents pixels de valeur 1 dans mask aux différents grains. Cette opération s’appelle la segmentation de l’image. Comme la phase de valeur 1 est continue (les grains se touchent), il n’y a pas d’opération simple permettant de faire cette séparation en une étape.

En consultant la gallerie du scikit-image, on peut voir qu’il y a justement un exemple où on sépare deux objets collés.

Cet exemple utilise un algorithme de segmentation appelé watershed (montée des eaux en français), implémenté dans la fonction skimage.morphology.watershed. Pour comprendre comment l’algorithme fonctionne, lire l’exemple et la docstring de la fonction watershed.

L’algorithme de watershed:

• part de pixels marqués comme appartenant à différents objets
• agit sur une image dont on considère les différents niveaux de gris comme des altitudes, et où les pixels marqués vont typiquement être dans les creux de cette carte d’altitude.
• fait grandir des régions à partir de ces pixels marqués, en remontant les niveaux de l’image d’entrée de l’algorithme. La propagation s’arrête quand deux régions se rencontrent.

7.1.3.3.1. Marqueurs

Il faut donc fournir à l’algorithme une image de marqueurs, où on aura identifé quelques pixels appartenant de manière certaine à chaque grain. Pour celà, on va éroder le masque jusqu’à séparer tous les grains. Il s’agit d’une opération typique de morphologie mathématique, qui se trouve donc dans le sous-module skimage.morphology. Une combinaison d’opérations d’érosion qui fonctionne bien est:

from skimage import morphology
erosion = morphology.binary_erosion(mask, morphology.disk(9))
erosion = morphology.binary_erosion(erosion, morphology.disk(5))

Afficher le tableau erosion après la 1e opération d’érosion, puis après la 2e. Essayer d’autres paramétres pour la taille de l’érosion : si on érode trop, on fait disparaître des grains, mais si on n’érode pas assez, certains grains vont rester attachés...

Une fois qu’on a séparé les grains, utiliser la fonction skimage.morphology.label pour donner un indice différent à chaque région de marqueurs. On appelera labs le tableau de marqueurs.

7.1.3.3.2. Carte d’élévation

Il faut maintenant créer une image où les minima correspondent à peu près à la position des marqueurs, et les régions les plus élévées aux séparations entre les grains. Pour celà, on va faire comme dans l’exemple du scikit-image : créér une image où la valeur de chaque pixel correspond à la distance du pixel au fonc dans le tableau mask. Ce tableau aura donc ses plus grandes valeurs au centre des disques, et ses plus petites valeurs au bord des grains : il faudra prendre l’opposé de ce tableau comme tableau d’entrée du watershed.

La fonction qui calcule la distance ne se trouve pas dans skimage, mais dans scipy.ndimage

>>> from scipy import ndimage
>>> ndimage.distance_transform_edt?

Appliquer cette fonction au tableau mask pour créer un tableau elevation_map.

7.1.3.3.3. Segmentation

On peut maintenant utiliser la fonction watershed sur le tableau elevation_map, avec comme tableau de marqueurs le tableau labs. Afin d’attribuer uniquement les pixels correspondant aux objets (et pas au fond), il faut également donner le tableau mask pour le keyword argument (argument optionnel) mask.

Calculer le résultat du watershed : appeler le résultat regions.

7.1.3.4. Propriétés des grains

Maintenant que nous avons séparé l’image en plusieurs régions, on peut calculer les propriétés des différentes régions. La fonction skimage.measure.regionprops sert justement à mesurer les propriétés d’une image de labels.

Calculer l’aire et le centroïde de chaque région avec cette fonction. La fonction regionprops renvoie une liste de dictionnaire, on peut boucler sur les éléments de la liste pour extraire à chaque dictionnaire la clé correspondant à l’aire et au centroïde.

Quel est la taille du plus petit grain ?

(Remarque - optionnel : pour bien faire les choses proprement, on peut mettre à 0 les régions correspondant aux bords du cadre de l’image. Utiliser des masques (tableaux booléens) pour celà. Si on supprime certaines régions, on peut réindicer les labels de manière à ce qu’ils restent consécutifs grâce à la fonction skimage.segmentation.relabel_from_one).

7.1.3.5. Nombre de voisins des grains

Nous voulons maintenant connaître les indices des voisins de chaque grain, c’est-à-dire des grains qui touchent ce grain. Pour cela, une solution est de dilater chaque grain (au sens de la morphologie mathématique) et de repérer les indices recouverts par la dilatation du grain.

Quelques indices :

• boucler sur les objets en créant des masques regions == lab pour les différents labels lab
• utiliser skimage.morphology.binary_dilation pour dilater ce masque.
• utiliser le masque dilaté pour extraire du tableau regions les valeurs des pixels recouverts par le masque.
• utiliser la fonction np.unique pour ne garder qu’une occurrence de chaque valeur.
• ajouter ces valeurs à un conteneur, par exemple une liste.

Quelle est la moyenne du nombre de voisins ? En deux dimensions, dans un milieu granulaire sans frottement à l’équilibre mécanique la moyenne du nombre de contacts est 4, pour assurer la condition d’iso-staticité. Dans cet exemple on devrait trouver moins, car les grains frottent entre eux.

Une fois qu’on a extrait les voisins, on peut tracer des liens entre voisins grâce à la fonction skimage.draw.line.

[La solution]