7.4. Cryptographie¶
Exercice 1: Cryptographie conventionnelle
- Dans un interpréteur Python créez la chaîne de caractères message contenant la valeur ‘ceci est mon message a chiffrer’. A l’aide d’une boucle for sur cette chaîne, chiffrer la par un décalage de 3 (chiffre de César). Par exemple la lettre a sera chiffrée en la lettre d (et la lettre x en la lettre a).
- Écrire un script Python qui chiffre (ou déchiffre selon le choix de l’utilisateur) une chaîne de caractères entrée au clavier avec une clé (i.e.un décalage) choisi aussi par l’utilisateur. On définira les fonctions chiffrer et dechiffrer.
- Modifier le script précédent pour qu’il utilise la méthode de chiffrement de Vigenère : la clé est désormais une chaîne de caractères et le chiffrement se fait en décalant la i-ème lettre du message gràce à la i-ème lettre de la clé (on reprend au début de la clef quand on a fini de lire celle-ci) suivant la règle naturelle A=1,B=2,...,Z=26.
- Modifier le script précédent pour qu’il chiffre/déchiffre un fichier dont le chemin est entré par l’utilisateur. On pourra utiliser cette nouvelle de Edgar Poe pour tester le script.
Exercice 2: Cryptanalyse fréquentielle
Comme expliqué dans la nouvelle de E. Poe, les chiffrements par substitution alphabétique peuvent être casser facilement par une analyse fréquentielle. Par exemple, dans un texte écrit en langue française, la lettre la plus fréquente est généralement le “E” et puisqu’un chiffrement de César ne modifie pas les fréquences, la lettre qui apparaît le plus fréquemment dans le texte chiffré correspond vraisemblablement à “E” et si c’est le cas le décalage entre les deux lettres donne la clé et permet de retrouver l’intégralité du message clair.
- Écrire une fonction Python qui prenant en entrée une chaîne de caractères (ou un fichier texte) affiche la fréquence des caractères qui le composent.
- Utiliser cette fonction pour créer une fonction qui prend un entrée un texte chiffré avec le chiffrement de César (mais pas la clé) et retourne un texte clair associé. On pourra demander à l’utilisateur de valider que ce texte est correct (et si ce n’est pas le cas proposer un nouveau texte clair probable).
- L’encyclopédie Wikipedia propose un article expliquant une méthode de cryptanalyse du chiffrement de Vigenère reposant sur les mêmes principes. Écrire une fonction Python qui prend un entrée un texte chiffré avec le chiffrement de Vigenère (mais pas la clé) et retourne un texte clair associé possible.
Exercice 3: Cryptographie à clé publique basée sur les courbes elliptiques
En mathématiques, une courbe elliptique est une courbe algébrique définie sur un corps 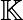 ,
unie entre autres propriétés, d’une loi de groupe définie sur l’ensemble de ses points.
,
unie entre autres propriétés, d’une loi de groupe définie sur l’ensemble de ses points.
Si la caractéristique du corps est différente de 2 et 3, une courbe elliptique est donnée par
l’équation de Weierstrass 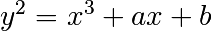 , où
, où 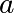 et
et 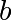 sont des éléments
du corps
sont des éléments
du corps 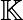 vérifiant
vérifiant 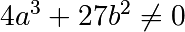 .
.
Nous considérons l’ensemble des points de la courbe
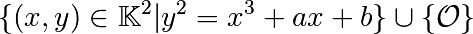
où  est un point sur la droite à l’infini (dans le plan projectif correspondant).
Ce point représente l’élément neutre pour la loi d’addition de la courbe.
est un point sur la droite à l’infini (dans le plan projectif correspondant).
Ce point représente l’élément neutre pour la loi d’addition de la courbe.
L’usage des courbes elliptiques en cryptographie a été proposé en 1986, indépendamment par Neal Koblitz et Victor Miller, pour l’instanciation des opérations cryptographiques asymétriques, comme l’échange de clé entre deux personnes sur un canal non-sécurisé. Par rapport aux systèmes fondés sur RSA, les systèmes de chiffrement sur les courbes elliptiques utilisent des clés plus courtes, pour un niveau de sécurité équivalent.
Par la suite, on considéra une courbe elliptique définie sur un un corps fini 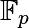 avec
avec 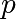 un nombre premier
un nombre premier  . Pour définir l’addition de deux points distincts
. Pour définir l’addition de deux points distincts 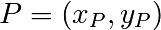 et
et
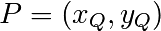 sur la courbe elliptique
sur la courbe elliptique 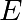 , on remarque d’abord que par ces deux points passe
une droite bien définie. Par le théorème de Bézout, cette droite recoupe la courbe
, on remarque d’abord que par ces deux points passe
une droite bien définie. Par le théorème de Bézout, cette droite recoupe la courbe 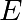 en un troisième point.
La somme des points
en un troisième point.
La somme des points 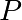 et
et 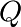 est alors donnée par le symétrique de ce point par rapport à l’axe
des abscisses. On donne maintenant des équations explicites pour calculer les coordonnées affines du point somme.
est alors donnée par le symétrique de ce point par rapport à l’axe
des abscisses. On donne maintenant des équations explicites pour calculer les coordonnées affines du point somme.
- Si
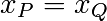 et
et 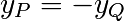 , alors
, alors 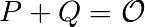 .
Autrement dit, l’inverse d’un point pour la loi du groupe est son symétrique
par rapport à l’axe des abscisses.
.
Autrement dit, l’inverse d’un point pour la loi du groupe est son symétrique
par rapport à l’axe des abscisses. - Sinon, on définit les quantités suivantes:
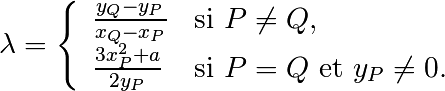
et
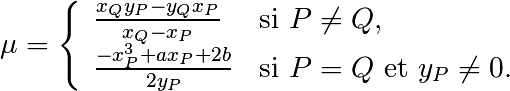
Alors la droite 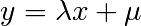 passe par
passe par 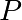 et
et 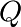 et les
coordonnées de
et les
coordonnées de 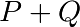 sont :
sont :
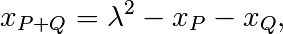
et
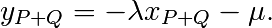
Loi d’addition sur la courbe elliptique. Soit
 la courbe elliptique donnée par l’équation
la courbe elliptique donnée par l’équation
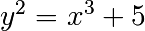 , définie sur le corps fini
, définie sur le corps fini 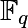 , avec
, avec 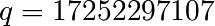 .
Le nombre de points sur cette courbe est
.
Le nombre de points sur cette courbe est 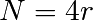 , avec
, avec 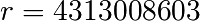 .
.Écrire une fonction qui calcule un point au hasard de la courbe. Indication: pour cela, on écrit d’abord une fonction calculant des racines carrées
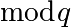 . On se rappelle que
lorsque
. On se rappelle que
lorsque 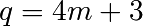 , la racine carrée de
, la racine carrée de 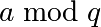 (quand elle existe) est
(quand elle existe) est
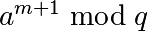 .
.Écrire une fonction qui calcule la somme des deux points de la courbe. On testera cette fonction à l’aide des exemples suivants (avec P=[6587596005,10930896470], Q=[2846256190,0], R=[1099048983,3110000776])
- P+Q=[10674847433,12569638509], P+R=[6587596005,6321400637]
- P+P=[1099048983,14142296331], Q+Q=O
- 3P=[8376961733,938225291], 5P=[1708109053,5741342158]
Écrire une fonction qui étant donné un point
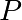 de la courbe, et un entier
de la courbe, et un entier 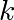 ,
calcule efficacement le point
,
calcule efficacement le point 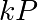 . Pour cela, on utilisera l’algorithme de
multiplication rapide (double and add ou square and multiply). On testera cette fonction sur
un point au hasard
. Pour cela, on utilisera l’algorithme de
multiplication rapide (double and add ou square and multiply). On testera cette fonction sur
un point au hasard 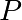 d’ordre
d’ordre 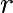 de la courbe (i.e.
de la courbe (i.e. 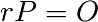 ).
).
Échange de clé Diffie-Hellman. Deux personnes, Alice et Bob, veulent échanger un message chiffré nécessitant une clé
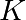 , qui est un nombre entier. Ils doivent échanger la clé
, qui est un nombre entier. Ils doivent échanger la clé 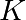 d’abord,
mais ils ne disposent pas de canal sécurisé pour cela. En 1976, Diffie et Hellman ont proposé une
méthode qui répond à ce problème. Le protocole de Diffie Hellman utilise un groupe cyclique
d’abord,
mais ils ne disposent pas de canal sécurisé pour cela. En 1976, Diffie et Hellman ont proposé une
méthode qui répond à ce problème. Le protocole de Diffie Hellman utilise un groupe cyclique 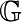 (noté additivement) d’ordre
(noté additivement) d’ordre 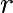 et repose sur l’idée suivante:
et repose sur l’idée suivante:- Étant donné un nombre entier
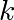 et un élément
et un élément 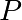 dans le groupe
dans le groupe 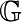 ,
il est facile de calculer
,
il est facile de calculer 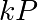 .
. - Étant donné
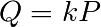 ,
, 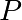 , il est calculatoirement difficile de retrouver
, il est calculatoirement difficile de retrouver 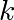
Le fonctionnement du protocole est le suivant. Alice choisit un nombre au hasard
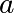 ,
calcule
,
calcule 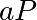 et l’envoie à Bob. Bob choisit à son tour un nombre
et l’envoie à Bob. Bob choisit à son tour un nombre 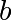 et envoie
à Alice
et envoie
à Alice 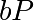 . Alice peut alors calculer
. Alice peut alors calculer 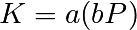 . Bob calcule
. Bob calcule 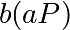 et
obtient la même clé
et
obtient la même clé 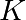 qu’Alice.
qu’Alice.- (Travail en binôme) En utilisant le groupe d’ordre
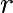 des points de la courbe
des points de la courbe 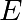 ,
échangez avec un collègue une clé secrete .
,
échangez avec un collègue une clé secrete .
- Étant donné un nombre entier
L’attaque pas de bébé, pas de géant sur le logarithme discret. La méthode de Shanks pour résoudre le problème du logarithme discret est basée sur l’observation suivante :
En notant
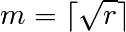 la partie entière supérieure de la racine carrée de
la partie entière supérieure de la racine carrée de 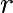 ,
on peut écrire tout élément
,
on peut écrire tout élément 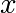 inférieur à
inférieur à 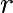 comme
comme 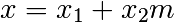 , avec
, avec
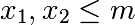 . Par conséquent, l’égalité
. Par conséquent, l’égalité 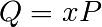 peut s’écrire
peut s’écrire 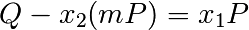 .
.Dans un premier temps (le pas de bébé), l’algorithme construit l’ensemble
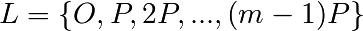 .
Dans un deuxième temps (le pas de géant), il calcule S=(-m)P puis recherche la valeur du membre de
droite de l’équation précédente dans la liste L
.
Dans un deuxième temps (le pas de géant), il calcule S=(-m)P puis recherche la valeur du membre de
droite de l’équation précédente dans la liste Lconstruire l'ensemble L = {O,P,2P,...,(m-1)P} pour i de 1 à m-1 faire si Q+iS est dans L alors retourner (j-im mod r) tel que jP=Q+iS.Pour chercher de manière efficace dans l’ensemble L on pourra utiliser une structure de dictionnaire.
- Implanter l’attaque de Shanks, afin de retrouver, à partir du point de la courbe qui vous a été envoyé, le secret de votre collègue.


