1. Introduction à Python et son environnement¶

1.1. Écosystème et environnement de travail¶

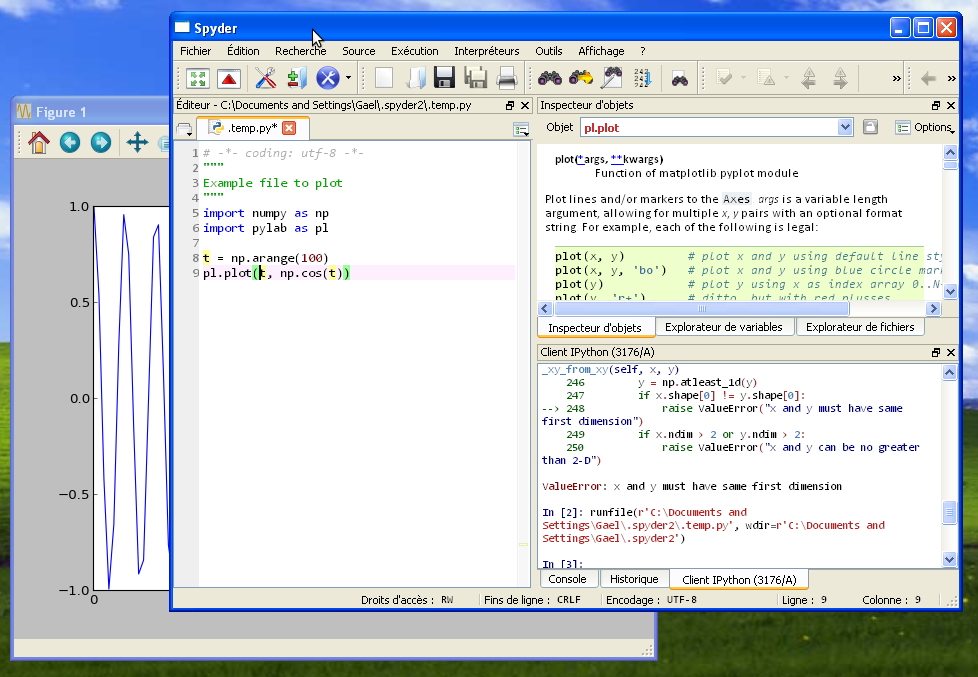
Environnement de travail scientifique spyder

Python est un langage de programmation très polyvalent et modulaire, qui est utilisé aussi bien pour écrire des applications comme YouTube, que pour traiter des données scientifiques. Par conséquent, il existe de multiples installations possibles de Python. L’utilisateur débutant peut donc se sentir dérouté par l’absence d’une référence unique pour Python scientifique. Nous conseillons donc un logiciel unique pour la formation, la suite scientifique Anaconda développée par l’entreprise Continuum. Anaconda rassemble tout le nécessaire pour l’enseignement de Python scientifique: le langage Python et ses modules scientifiques.

En particulier, Anaconda fournit un environnement de travail adapté à l’enseignement et au calcul scientifique, spyder, que nous utiliserons pour la formation.

1.1.1. Installation de l’environnement Python scientifique¶

1.1.2. L’écosystème Python scientifique¶

Pour le calcul scientifique il faut utiliser Python 2.

Python:	Langage + librairie standard très riche Enseignement algorithmique (hash cryptographiques, piles partiellement ordonnées, décimaux de taille arbitraire) TIPE (manipulation de fichiers, calcul parallèle, téléchargement de données).
numpy:	Calcul de tableau et calcul matriciel
scipy:	Outils numériques standards: FFT, intégration, résolution de système non-linéaires
matplotlib:	Tracé de courbes et affichage scientifique

Tout est libre, développé en grande partie par des individus sur leur temps libre.

1.1.3. Un environnement de travail: Spyder¶

Pour lancer spyder:

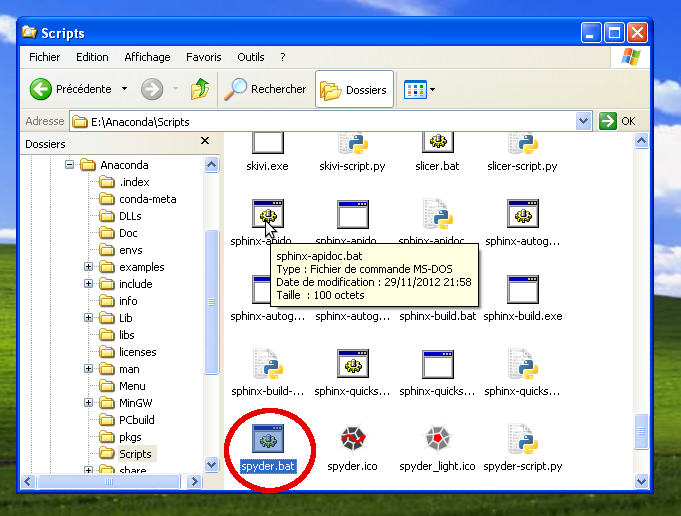
Sous windows exécuter Anaconda\Scripts\spyder.bat
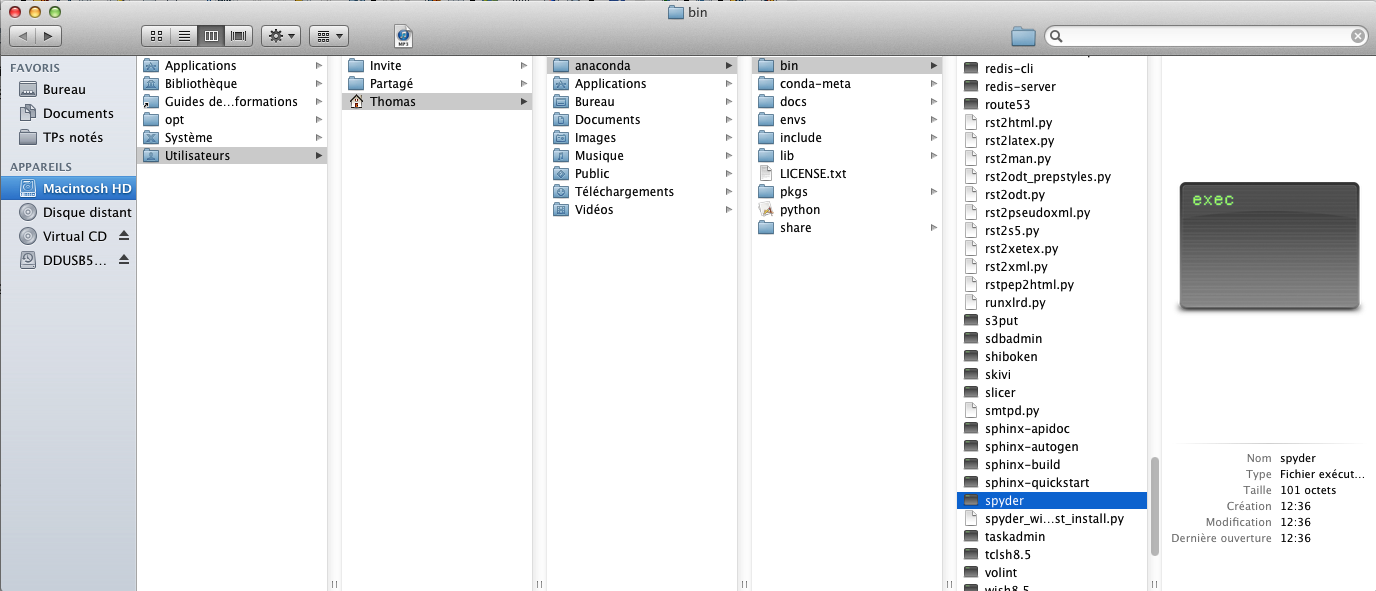
Sous Mac et Linux exécuter Anaconda/bin/spyder

Spyder présente 2 panneaux que nous allons beaucoup utiliser: en bas à droite, un interpréteur interactif Python, à gauche un éditeur pour écrire ses scripts Python.

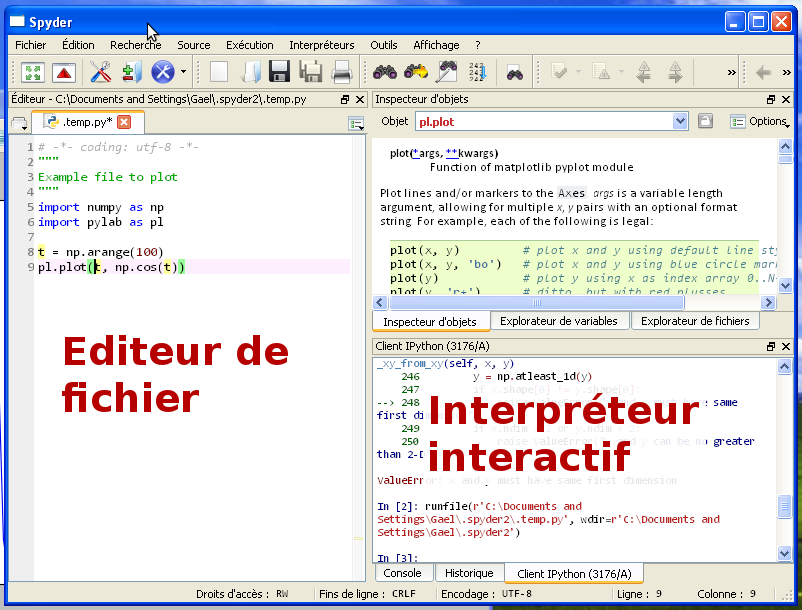
1.1.3.1. Configurer l’environnement¶

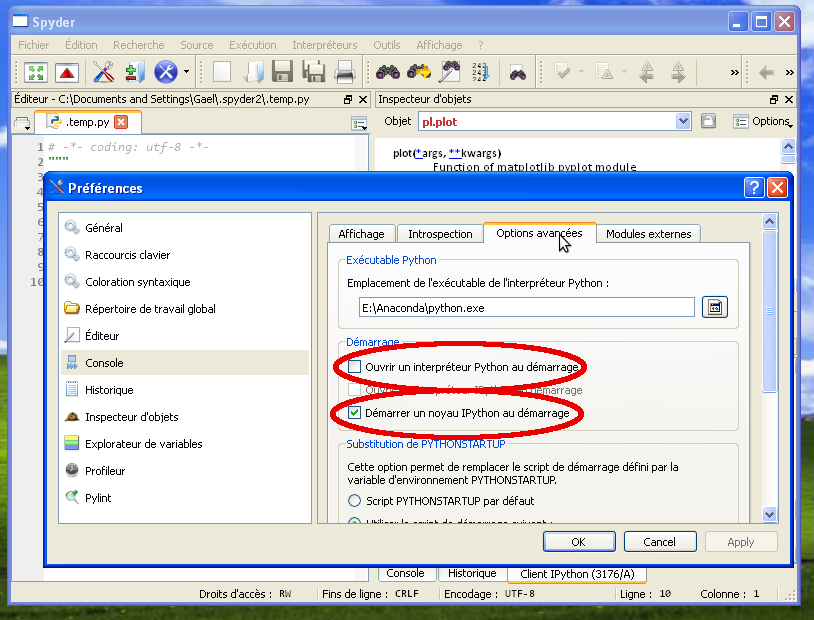
Nous voulons configurer le panneau de droite pour utiliser l’outil “IPython”, qui permettra la visualisation interactive de données:

Aller dans les menus Outils -> Préférences et dans la boite de dialogue correspondante, dans la section Console -> Options avancées, décocher “Ouvrir un interpréteur Python au démarrage”, et cocher “Démarrer un noyau IPython au démarrage”.

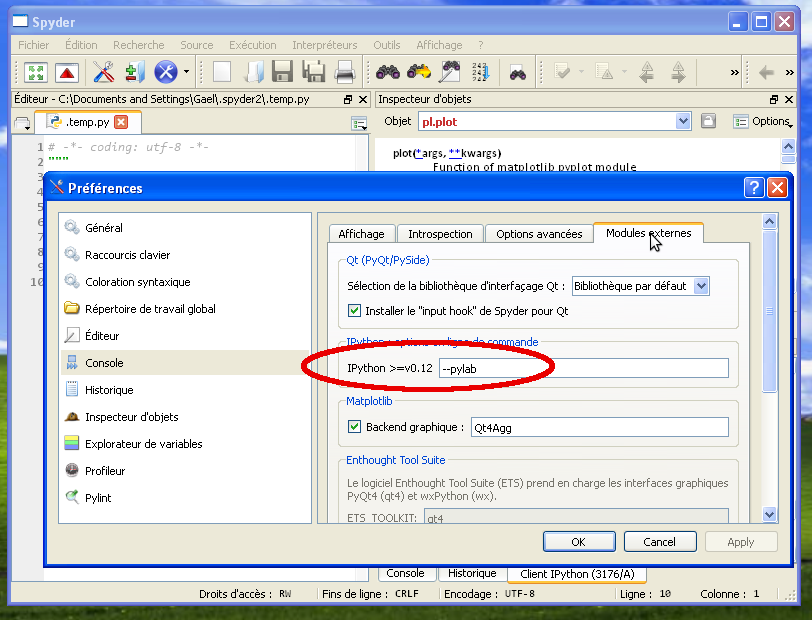
Dans l’onglet ‘Modules externes’, remplacer les options de la ligne de commande par ‘–pylab’.

1.1.3.2. Premiers pas¶

Dans l’interpréteur (panneau de droite), taper ‘1 + 1’:

>>> 1+1
2

Dans l’éditeur (panneau de gauche), ajouter la ligne:

print(1+1)

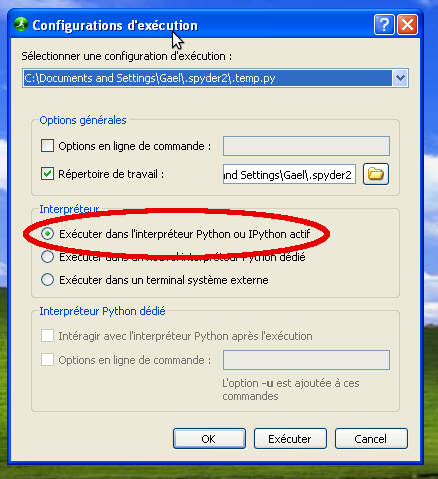
Puis, dans le menu ‘Exécution’, sélectionner ‘Exécution’, ou appuyer sur la touche ‘F5’. Dans le dialogue qui s’affiche ‘Configurations d’exécution’, sélectionner ‘Exécuter dans l’interpréteur Python ou IPython actif’.

1.2. Le langage Python¶

1.2.1. Différents type d’objets¶

1.2.1.1. Objets simples¶

>>> a=1
>>> b='Bonjour'

a et b sont des objets de différent types : a est un entier (int), et b est une chaîne de caractères (string).

En Python, les types ne sont pas déclarés explicitement.

Nombres	Entier 1 — Flottant 1. — Complexe 1 + 1j — Booléen False
Chaînes de caractère	Chaînes ‘Bonjour’ — Chaînes avec accents u’Gaël’

A différents types d’objets, correspondent différentes opérations possibles:

>>> 2*a
2

Remarque

Puissance:

>>> 2**3

Attention

Division entière

>>> 1/2
0
>>> 1./2
0.5
>>> float(1)/2
0.5

1.2.1.2. Collections d’objets¶

Listes
```
>>> l = [0, 1, 2, 3]
>>> l[0]
0
```
Attention

Les indices commencent à 0, et non à 1

On peut compter à partir de la fin en indexant une liste:
```
>>> l[-1]
3
```
Et on peut avoir des “tranches” d’une liste (“slice” en anglais):
```
>>> l[1:3]
[1, 2, 3]
```
La syntaxe du “slicing” est start:stop:step.

Une liste peut être modifiée:
```
>>> l[0] = -1
>>> l
[-1, 1, 2, 3]
>>> l.append(4)
>>> l
[-1, 1, 2, 3, 4]
```
Remarque

Les listes sont donc des objets “mutables”.
Remarque

l.append est une “méthode” de l.

Les méthodes de l peuvent être découverte en appuyant sur Tab dans IPython:
```
In [2]: l.
append  count  extend  index  insert  pop  remove  reverse  sort
```
Pour savoir ce qu’une méthode fait:
```
In [2]: l.append?
Type:       builtin_function_or_method
String Form:<built-in method append of list object at 0x34fa128>
Docstring:  L.append(object) -- append object to end
```
Une liste peut contenir des objets de type différents:
```
>>> l = [1, 2., 'hello', ['a', 'b']]
```
C’est donc un objet très polyvalent. Pour contenir un ensemble de nombres de même type, nous verrons plus tard un objet plus efficace (pour la rapidité d’exécution) : les tableaux numériques du module NumPy.

Finalement, pour créer une liste d’entiers continus:
```
>>> l = range(10)
>>> print l
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
```

Et plus encore

dictionnaires:

dictionnaires:	>>> d = {"Gael": "Informatique", "Werner": "Physique", "Emmanuelle": "Physique"} >>> d["Damien"] = "Informatique" >>> d["Gael"] "Informatique
tuple:	Comme une liste, mais non mutable: >>> l = (0, 1, 2, 3) >>> l[0] = -1 --------------------------------------------------------------------------- TypeError Traceback (most recent call last) <ipython-input-4-2c4c55c1f409> in <module>() ----> 1 l[0] = -1 TypeError: 'tuple' object does not support item assignment
set:	Ensemble d’éléments uniques muni d’opérations comme l’intersection ou l’union.

>>> d={"Gael":"Informatique","Werner":"Physique","Emmanuelle":"Physique"}
>>> d["Damien"]="Informatique"
>>> d["Gael"]
"Informatique

tuple:

Comme une liste, mais non mutable:

>>> l=(0,1,2,3)
>>> l[0]=-1
---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
<ipython-input-4-2c4c55c1f409> in <module>()
----> 1 l[0] = -1
TypeError: 'tuple' object does not support item assignment

set:

Ensemble d’éléments uniques muni d’opérations comme l’intersection ou l’union.

1.2.2. Logique du programme: opérations conditionnelles et boucles¶

Opérations conditionnelles
```
>>> a = 1
>>> if a == 1:
...     print('a vaut bien 1')
... else:
...     print('a ne vaut pas 1')
```
Remarque

== est différent de =. Le premier est un “test” et le deuxième une “affectation de variable”.
Remarque

L’indentation délimite les blocs logiques, elle est

obligatoire.
```
>>> if a == 1:
...     print('a vaut bien 1')
...     print("c'est certain")
```
Remarque

Pour taper des instructions sur plusieurs lignes, l’éditeur de texte (panneau gauche de spyder) est plus pratique.

Conditions multiples: a == 1 and b == 1, a == 1 or b == 1

Autres conditions: a != 1 (a différent de 1), a < 1, a > 1

Boucles

>>> foriinrange(3):
... print(i)
0
1
2

On peut itérer sur les éléments d’une liste:

>>> l=[0,1,2]
>>> foriinl:
... printi
0
1
2

Exercice: Calculer Pi avec la formule de Wallis

$\pi = 2 \prod_{i=1}^{\infty} \frac{4i^2}{4i^2 - 1}$

[La solution]

1.2.3. Définir des fonctions¶

deff(x,y):
printx
returnx+y

Arguments optionnels:

deff(x,y=1):
returnx+y
z=f(x,y=2)

1.2.4. Importer des fonctionnalités additionnelles¶

Les “modules” permettent d’importer de nombreuses fonctionnalités additionnelles, allant de modules d’interface graphique au calcul scientifique.

Voici un exemple qui importe un nouveau type de nombre, les fractions:

>>> importfractions
>>> a=fractions.Fraction(2,3)
>>> printa
2/3
>>> b=fractions.Fraction(1,2)
>>> printb
1/2
>>> a+b
Fraction(7, 6)
>>> printa+b
7/6

Voir aussi

Scipy Lecture Notes, chapitre sur le langage Python
Ouvrage de Gérard Swinnen: Apprendre à programmer avec Python
Documentation officielle du langage Python

Exercice: Implémenter quicksort

La page wikipedia décrivant l’algorithme de tri quicksort donne le pseudo-code suivant:

function quicksort('array')
   if length('array') <= 1
       return 'array'
   select and remove a pivot value 'pivot' from 'array'
   create empty lists 'less' and 'greater'
   for each 'x' in 'array'
       if 'x' <= 'pivot' then append 'x' to 'less'
       else append 'x' to 'greater'
   return concatenate(quicksort('less'), 'pivot', quicksort('greater'))

Saurez vous transformer ce pseudo-code en code valide Python.

Des indices:

La longueur d’une liste est donnée par len(l)

Deux listes peuvent être concaténées avec l1 + l2

l.pop() retire le dernier élément d’une liste

Attention: une liste est mutable

Il vous suffit de compléter cette ébauche:

defquicksort(l):
# ...
returnl
l=[3,4,1,2,5,6]
printquicksort(l)

[La solution]

1.2.5. Travailler avec beaucoup de nombres¶

Lorsque l’on fait du calcul scientifique, on doit souvent travailler avec de gros ensemble de nombres. Par example, calculons ici les racines carrées des 10 millions premiers entiers:

>>> N=1000000
>>> l=range(N)
>>> ll=[]# La liste vide, pour stoquer le résultat
>>> importmath# L'opération racine carré est définit dans le module math
>>> foriinl:
... ll.append(math.sqrt(i))

Notez que vous devez attendre un peu que cette boucle s’exécute.

En calcul scientifique, la manière efficace de travailler et d’utiliser les tableaux

>>> importnumpyasnp
>>> l=np.arange(N)# l est alors un tableau (array) et non une liste
>>> ll=np.sqrt(l)# En utilisant 'sqrt' du module numpy, l'opération est réalisée en block

Le module numpy est central au calcul scientifique. Nous le verrons plus en détail plus tard.

1.2.6. Comprendre les erreurs¶

Lorsque Python rencontre une situation dont il ne sait se sortir, il lève une erreur (exception en jargon):

In [1]: 1 + 'a'
---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call
last)
<ipython-input-1-bb4aa3e60e23> in <module>()
----> 1 1 + 'a'

TypeError: unsupported operand type(s) for +: 'int' and 'str'

Ici c’est une erreur de ‘type’: Python ne sait additionner des entiers et des chaînes de caractère.

In [2]: l = [0, 1]

In [3]: l[2]
---------------------------------------------------------------------------
IndexError                                Traceback (most recent call last)
<ipython-input-3-5b08617e4833> in <module>()
----> 1 l[2]

IndexError: list index out of range

Une erreur d’indexation : j’ai donné un indice trop grand pour la liste.

Regardez bien le message d’erreur, il vous en dit beaucoup: de quelle erreur il s’agit, et où elle s’est produite

In [4]: def f(x):
...:     y = 1. / (1 = x)
...:     return y
...:
File "<ipython-input-4-782a072b3f3f>", line 2
    y = 1. / (1 = x)
                ^
SyntaxError: invalid syntax

In [5]: def f(x):
    y = 1. / (1 + x)
    return y
...:


In [6]: f(-1)
---------------------------------------------------------------------------
ZeroDivisionError                         Traceback (most recent call last)
<ipython-input-6-512b55eb878d> in <module>()
----> 1 f(-1)

<ipython-input-5-9ac7ba330cae> in f(x)
    1 def f(x):
----> 2     y = 1. / (1 + x)
    3     return y

ZeroDivisionError: float division by zero

Navigation

1. Introduction à Python et son environnement¶

1.1. Écosystème et environnement de travail¶

1.1.1. Installation de l’environnement Python scientifique¶

1.1.2. L’écosystème Python scientifique¶

1.1.3. Un environnement de travail: Spyder¶

1.1.3.1. Configurer l’environnement¶

1.1.3.2. Premiers pas¶

1.2. Le langage Python¶

1.2.1. Différents type d’objets¶

1.2.1.1. Objets simples¶

1.2.1.2. Collections d’objets¶

1.2.2. Logique du programme: opérations conditionnelles et boucles¶

1.2.3. Définir des fonctions¶

1.2.4. Importer des fonctionnalités additionnelles¶

1.2.5. Travailler avec beaucoup de nombres¶

1.2.6. Comprendre les erreurs¶

Navigation