2. Structures de données en Python. Un exemple de la théorie de l’information

2.1. Modules et fichiers

2.1.1. Modules

On peut ranger les définitions de fonctions se rapportant à une même application au sein d’un script commun baptisé module

Un module est sauvegardé sous forme d’un fichier dont le nom a la forme <nom du module>.py

Pour utiliser un module, il faut se servir de l’instruction

import <nom du module>

L’exécution de cette instruction consiste à exécuter le script définissant le module (ce script peut contenir des instructions autres que des définitions de fonctions).

Pour importer un module, Python a besoin de connaître le chemin qui permet d’accéder au fichier correspondant. Ce chemin doit apparaître dans la liste des chemins possibles stockés dans la variable path du module sys

Première méthode d’importation

>>> import random
>>> random.randint(0,10)
9

• L’instruction import permet d’importer toutes les fonctions du module random
• Ensuite, nous utilisons la fonction (ou méthode) randint(a,b) du module random; attention cette fonction renvoie un nombre entier aléatoirement entre a inclus et b inclus

Deuxième méthode d’importation

Pour disposer d’une fonction du module

from [module] import [fonction]

Pour disposer de toutes les fonctions d’un module

from [module] import *

Remarque

Cette option est cependant à éviter notament lorsqu’un module propose un nombre important de fonctions et parce que certains modules ont des fonctions qui ont le même nom (par exemple, math et numpy)

from math import *
sept = sqrt(49)
angle = pi/6
print sin(angle)

---

Modules courants

• sys : passage d’arguments, gestion de l’entrée/sortie standard etc...
• os : dialogue avec le système d’exploitation.
• math : fonctions et constantes mathématiques de base (sin, cos, exp, pi...).
• random : génération de nombres aléatoires.
• time : permet d’accéder aux fonctions gérant le temps.
• urllib : permet de récupérer des données sur internet depuis python.
• re : gestion des expressions régulières.
• numpy, scipy: modules incontournables du calcul scientifique
• Tkinter : interface graphique
• ...

2.1.2. Fichiers

Pour permettre une interaction avec l’utilisateur, la méthode la plus simple consiste à employer la fonction raw_input() :

print('Entrez votre prénom : ')
prenom = raw_input()
print 'Bonjour,', prenom

prenom = raw_input('Entrez votre prénom : ')
print 'Bonjour,', prenom

Remarque

La fonction raw_input() renvoie toujours une chaîne de caractères alors que la fonction input() renvoie une valeur dont le type correspond à ce que l’utilisateur a entré`(i.e. une chaîne de caractères doit être entrée avec des guillemets).

Il est généralement important de dissocier les données des programmes qui les utilisent en rangeant ces données dans des fichiers séparés.

Le module os contient des fonctions qui permettent de localiser les fichiers :

• getcwd() : Retourne le chemin du répertoire courant
• chdir(<ch>) : Change le répertoire courant qui prend la valeur donnée par la chaîne <ch>
• path.isfile(<ch>) : Retourne un booléen qui indique s’il existe un fichier de chemin <ch>
• path.isdir(<ch>) : Retourne un booléen qui indique s’il existe un répertoire de chemin <ch>

from os import chdir
chdir("/home/exercices")

Remarque

En mode interactif, iPython reconnaît les commandes consoles traditionnelles (ls, cd, pwd, ...)

Pour utiliser un fichier identifié par le chemin <ch> dans un programme Python, il faut commencer par l’ouvrir par l’appel de fonction

open(<ch>, [<mode>])

qui retourne un objet de type file.

Le paramètre facultatif <mode> indique le mode d’ouverture du fichier :

• r : mode lecture (le fichier doit exister préalablement)
• w : mode écriture (si le fichier existe, les données sont écrasées, sinon le fichier est créé)
• a : mode ajout (si le fichier existe, les données écrites vont l’être après celles existantes, sinon le fichier est créé)

Si le mode est omis, le mode par défaut est r.

Un objet de type file est associé à des attributs et des méthodes. En voici quelques-unes :

• read([<n>]) : retourne la chaîne des <n> caractères restants
• readline() : lit une seule ligne à partir du fichier
• readlines() : utilise f.readline() de façon répétitive, et retourne une liste contenant toutes les lignes du fichier.
• write(<ch>) : écrit la chaîne de caractères <ch>
• close() : ferme le fichier
• seek(<n>) : choisit le caractère <n> comme position courante du fichier
• tell() : retourne le caractère en position courante

# Exemple de copie intégrale d'un fichier
fs = open("source.txt", 'r')
fd = open("destination.txt", 'w')
while 1:
    txt = fs.read(50) # copie de 50 caractères à la fois
    if txt == "":
        break
    fd.write(txt)
fs.close()
fd.close()

Remarque

Python fournit le module standard pickle qui peut prendre (presque) n’importe quel objet Python et le convertir en une représentation sous forme de chaîne de caractères (et le reconstruire). Il s’agit du moyen standard pour enregistrer des objets Python et les réutiliser dans d’autres programmes.

2.2. Structures de données en Python

2.2.1. Utilisation avancée des listes

Les fonctions héritées du fonctionnel. La fonction map permet de transformer une liste via l’utilisation d’une fonction. Elle prend en entrée une fonction et une liste et retourne une nouvelle liste en appelant la fonction sur chaque élément de la liste dans l’ordre. Voici quelques exemples d’utilisation :

def carre(x):
    return x ** 2
def pair(x):
    return not bool(x % 2)

print map(carre, [1, 2, 3, 4, 5])
# Affiche [1, 4, 9, 16, 25]

print map(pair, [1, 2, 3, 4, 5])
# Affiche [False, True, False, True, False]

Comme dans les langages fonctionnels, avec le mot-clé lambda, il est possible de créer des fonctions anonymes. Le premier exemple est équivalent à

print map(lambda x: x**2, [1, 2, 3, 4, 5])
# Affiche [1, 4, 9, 16, 25]

La fonction filter permet de retirer les valeurs d’une liste que l’on ne veut pas. Elle prend en entrée une fonction et une liste et retourne la liste des éléments (dans l’ordre) sur lesquels la fonction retourne le booléen True.

def petit_carre(x):
    return x ** 2 < 16
def pair(x):
    return not bool(x % 2)

print filter(petit_carre, [1, 2, 3, 4, 5])
# Affiche [1, 2, 3]

print filter(pair, [1, 2, 3, 4, 5])
# Affiche [2, 4], c'est à dire les nombres pairs de la liste.

Les compréhensions de liste. Les compréhensions de liste sont des outils puissants permettant d’utiliser map et filter avec une syntaxe plus proche de celle habituelle en Python. De plus, elles permettent de combiner un map et un filter en même temps.

Voici la syntaxe avec les exemples vus précédemment

# Affiche les carrés des éléments
liste = [1, 2, 3, 4, 5, 6, 7]
print [x ** 2 for x in liste]
# Équivaut au map, en plus lisible et plus simple :) .

# Affiche les nombres pairs
print [x for x in liste if x % 2 == 0]
# Plus simple que filter, également :)

# Affiche les carrés pairs (combinaison des deux)
print [x ** 2 for x in liste if x ** 2 % 2 == 0]
# ou print [x for x in [a ** 2 for a in liste] if x % 2 == 0]

Méthodes supplémentaires sur les listes

Voici une liste des méthodes des objets de type liste les plus utiles :

L.append(x):

Ajoute l’élément x à la fin de la liste L

L1.extend(L2):

Étend la liste L1 en y ajoutant tous les éléments de la liste L2

L.insert(i, x):

Insère l’élément x dans la liste L à la position i

L.remove(x):

Supprime de la liste L le premier élément dont la valeur est x.

L.pop([i]):

Enlève de la liste L l’élément situé à la position i

Si aucune position n’est indiqué, L.pop() enlève et retourne le dernier élément de la liste

L.index(x):

Retourne la position du premier élément de la liste L ayant la valeur x.

L.sort():

Trie les éléments de la liste, en place.

L.reverse():

Inverse l’ordre des éléments de la liste, en place.

Remarque

Ces méthodes permettent d’utiliser les listes comme des piles (i.e. une structure de donnée “dernier entré, premier sorti” ou LIFO) L’ajout d’un élément sur la pile se fait avec la méthode append() et la méthode pop() permet de récupérer l’objet au sommet de la pile. Cependant, les listes ne sont pas adaptées pour implanter des files (i.e. une structure de donnée “dernier entré, dernier sorti” ou FIFO) pour lesquelles il vaut mieux utiliser la classe collections.deque.

2.2.2. Un exemple de structures de donnée complexe : Le tas

Tas binaire. Un tas binaire (en anglais, heap) est une structure de données qui :

• est un arbre binaire
• est ordonné de sorte que la clé d’un nœud est toujours inférieure à la clé de ses fils (de sorte que son plus petit élément est toujours la racine de l’arbre).

Les tas binaires supportent les opérations suivantes :

• Construire-Tas
• Ajouter-Élément
• Consulter-Sommet
• Retirer-Élément
• Tamiser (refabriquer le tas pour qu’il retrouve ses propriétés; par exemple suite à l’ajout ou la suppression d’un élément)

Les tas permettent notamment d’implanter les files de priorité qui permettent d’effectuer les trois opérations suivantes :

• insérer un élément
• lire puis supprimer l’élément ayant la plus grande clé
• tester si la file de priorité est vide ou pas

Module heapq. Ce module propose une implantation efficace des tas binaires (et des files de priorité) qui utilise naturellement des tableaux.

import heapq

Les fonctions suivantes sont notamment définies :

heapq.heappush(T, x):  Ajoute la valeur x au tas T (en conservant la propriété de tas) heapq.heappop(T):  Enlève et retourne le premier élément du tas T heapq.heapify(L):  Transforme la liste L en un tas (en place et en temps linéaire)

Remarque

En pratique, puisque un tas est un arbre binaire, l’implantation utilise des tableaux unidimensionel de sorte que tas[k] <= tas[2*k+1] et tas[k] <= tas[2*k] pour tout k. En particulier le père d’un noeud en position k a pour position (k-1)/2 et les fils d’un noeud en position k sont situés aux positions 2*k et 2*k+1.

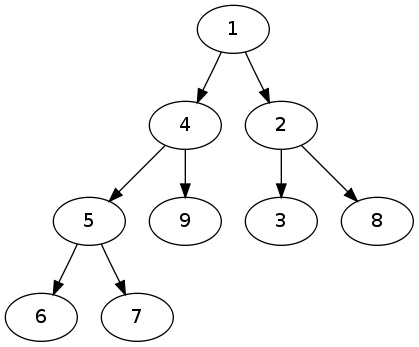
In [1]: from heapq import *

In [2]: L = [7,4,8,1,9,3,2,6,5]

In [3]: heapify(L)

In [4]: L
Out[4]: [1, 4, 2, 5, 9, 3, 8, 6, 7]

2.3. Codage de Huffman

2.3.1. Principe

Le codage de Huffman est une méthode de compression de données sans perte proposé par David Huffman en 1952. Elle consiste à attribuer un mot binaire de longueur variable aux différents symboles du document à compresser (pixels ou caractères par exemple). Les symboles les plus fréquents sont codés avec des mots courts, tandis que les symboles les plus rares sont encodés avec des mots plus longs (rappelant ainsi le principe de l’alphabet Morse). Le code construit a la particularité de ne posséder aucun mot ayant pour préfixe un autre mot (i.e. il s’agit d’un code préfixe).

Le codage de Huffman crée un arbre binaire à partir de tous les symboles et de leur nombre d’occurrences dans le document :

• chaque caractère constitue une des feuilles de l’arbre à laquelle on associe un poids valant son nombre d’occurrences
• l’arbre est créé récursivement en associant à chaque étape les deux nœuds de plus faibles poids pour donner un nœud dont le poids est égal à la somme des poids de ses fils jusqu’à n’en avoir plus qu’un, la racine.

L’utilisation d’un tas pour construire cet arbre est donc particulièrement appropriée.

On associe ensuite le code 0 à la branche de gauche et le code 1 à la branche de droite et le code binaire de chaque symbole est alors obtenu en parcourant la racine jusqu’à la feuille et en notant le parcours (0 ou 1) à chaque noeud.

Un arbre d’Huffman associé au texte “PROGRAMMATION EN LANGAGE PYTHON” est donné sur la figure suivante :

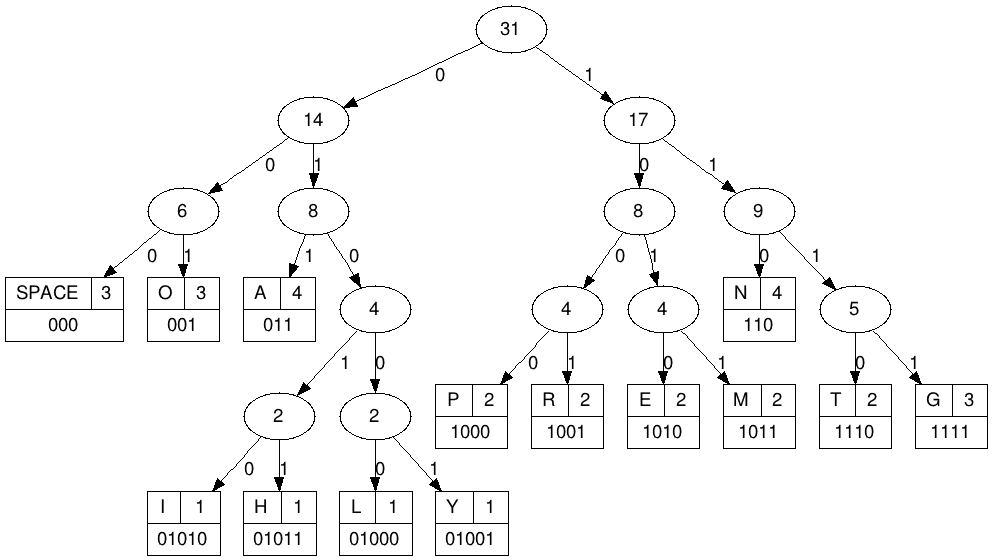
La lettre “A” avec 4 occurrences est codée par le triplet 011 alors que la lettre Y plus rare est codée par le mot de 5 bits 01001.

2.3.2. Implantation du codage de Huffman en Python

Table des occurrences. La première étape de la méthode de compression de Huffman consiste à compter le nombre d’occurrences de chaque symbole.

Exercice: Construire une table des occurrences

Écrire une fonction table_frequences qui étant donné une chaîne de caractère texte retourne un dictionnaire qui associe à chaque caractère son nombre d’occurrences dans texte.

Le prototype de la fonction sera le suivant

def table_frequences(texte):

et

table_frequences("ABRACADABRA")

devra retourner un dictionnaire de la forme

{'A': 5, 'R': 2, 'B': 2, 'C': 1, 'D': 1}

Solution:

def table_frequences(texte):
    table = {}
    for caractere in texte:
        if caractere in table:
            table[caractere] = table[caractere] + 1
        else:
            table[caractere] = 1
    return table

Arbre de Huffman. Une approche naturelle pour construire l’arbre de Huffman à partir de la table des occurrences consiste à utiliser un tas binaire.

Dans un premier temps, on peut construire un tas correspondant à la table des occurrences (qui aura donc le caractère le moins fréquent à la racine). Ensuite, il faut utiliser cette structure pour construire récursivement l’arbre binaire :

• en recherchant les deux noeuds de plus petit poids (en utilisant la structure de tas)
• en fusionnant ces deux noeuds en un seul :
  • dont le poids est égal à la somme des poids des deux noeuds
  • qui a ces deux noeuds comme fils

Une représentation possible pour le noeud ainsi construit est d’utiliser un dictionnaire à deux clés (par exemple 0 pour gauche et 1 pour droite) dont les valeurs sont les représentations des noeuds initiaux.

Exercice: Construire un arbre de Huffman

Écrire une fonction arbre_huffman qui étant donné un dictionnaire construit par la fonction précédente retourne une représentation de l’arbre de Huffman correspondant.

Le prototype de la fonction sera le suivant

def arbre_huffman (occurrences):

et l’appel de

arbre_huffman(table_frequences("ABRACADABRA"))

devra retourner un dictionnaire de la forme

{0: 'A', 1: {0: 'R', 1: {0: {0: 'C', 1: 'D'}, 1: 'B'}}}

def arbre_huffman(occurrences):
    # Construction d'un tas avec les lettres sous forme de feuilles
    tas = [(occ, lettre) for (lettre, occ) in occurrences.items()]
    heapify(tas)

    # Création de l'arbre
    while len(tas) >= 2:
        occ1, noeud1 = heappop(tas) # noeud de plus petit poids occ1
        occ2, noeud2 = heappop(tas) # noeud de deuxième plus petit poids occ2
        heappush(tas, (occ1 + occ2, {0: noeud1, 1: noeud2}))
        # ajoute au tas le noeud de poids occ1+occ2 et avec les fils noeud1 et noeud2

    return heappop(tas)[1]

Code de Huffman

Exercice: Code de Huffman

Écrire une fonction code_huffman qui étant donné un arbre de Huffman construit par la fonction précédente retourne un dictionnaire où les clés sont les chaînes binaires et les valeurs les caractères correspondants.

Le prototype de la fonction sera le suivant

def code_huffman(arbre):

et l’appel de

C = code_huffman(T)
print T

avec T l’arbre précédent, devra retourner un dictionnaire de la forme suivante

{'10': 'R', '111': 'B', '0': 'A', '1100': 'C', '1101': 'D'}

def code_huffman_parcours(arbre,prefixe,code):
    for noeud in arbre:
        if len(arbre[noeud]) == 1:
            code[prefixe+noeud] = arbre[noeud]
        else:
            code_huffman_parcours(arbre[noeud],prefixe+noeud,code)

def code_huffman(arbre):
    code = {}
    code_huffman_parcours(arbre,'',code)
    return code

Encodage et décodage

Exercice: Encodage

Écrire une fonction encodage qui étant donné un code de Huffman construit par la fonction précédente et le texte initial retourne la chaîne de bits produite par le codage de Huffman.

Le prototype de la fonction sera le suivant

def encodage(code,texte):

et l’appel de

encodage(C,"ABRACADABRA")

avec C le code précédent, devra retourner la chaîne binaire suivante

"01111001100011010111100"

Solution:

def encodage(texte,code):
    code_inv = dict((code[bits], bits) for bits in code)
    # construit le dictionnaire inverse
    texte_binaire = ''
    for c in texte:
        texte_binaire = texte_binaire + code_inv[c]
    return texte_binaire

Exercice: Décodage

Écrire une fonction decodage qui étant donnés un code de Huffman et un texte binaire compressé retourne le texte initial.

Le prototype de la fonction sera le suivant

def decodage(code,texte_binaire):

et l’appel de

encodage(T,"01111001100011010111100")

avec C le code précédent, devra retourner la chaîne binaire suivante

"ABRACADABRA"

Solution:

def decodage(code,texte_binaire):
    texte = ''
    tampon = ''
    for b in texte_binaire:
        tampon = tampon+b
        if tampon in code:
            texte = texte+code[tampon]
            tampon = ''
    return texte